Lý thuyết Khái niệm hàm số và đồ thị của hàm số SGK Toán 8 - Kết nối tri thức
Hàm số là gì?
1. Hàm số
Khái niệm:
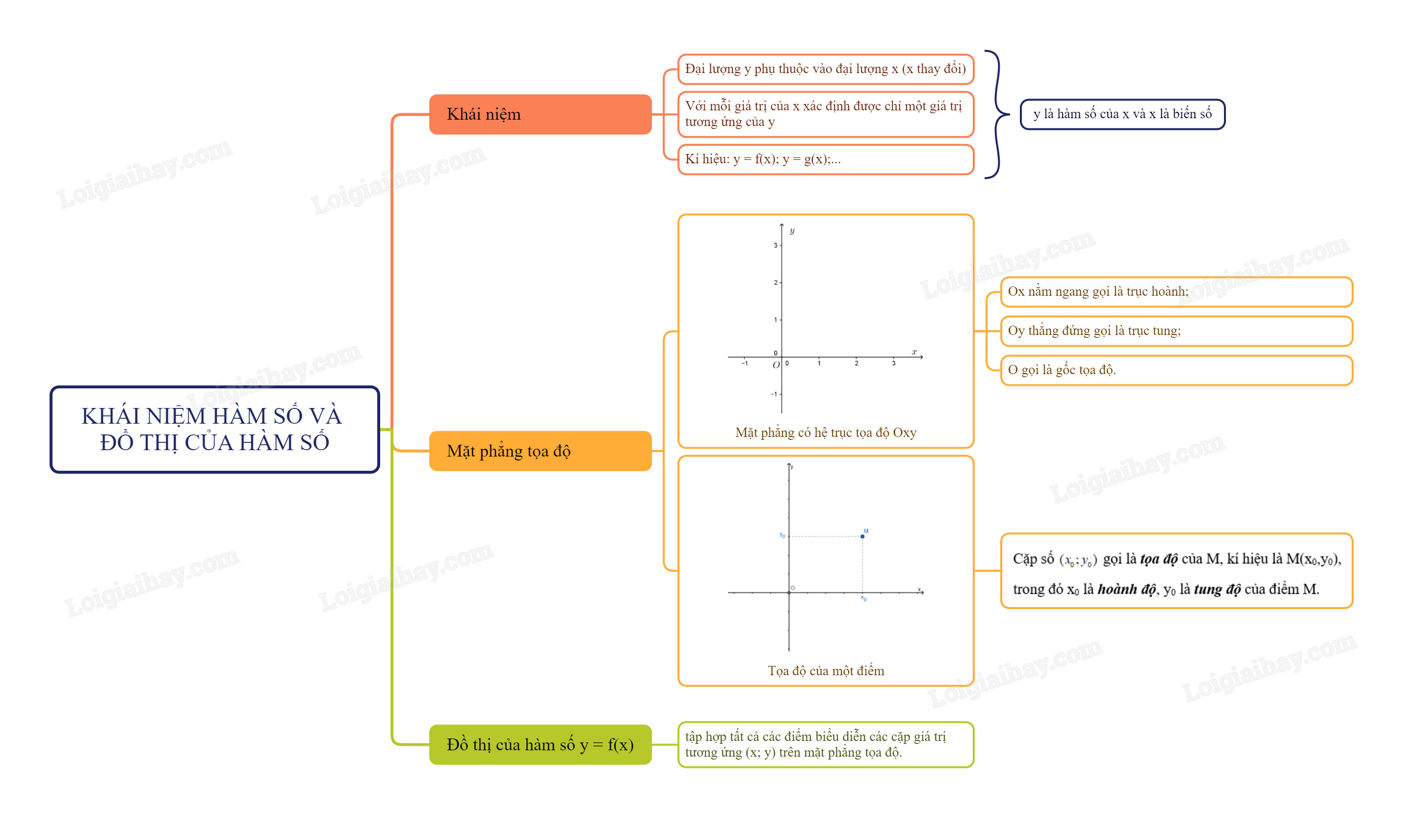
Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x sao cho với mỗi giá trị của x ta luôn xác định được chỉ một giá trị tương ứng của y thì y được gọi là hàm số của x và x gọi là biến số.
Ví dụ: Ta có bảng nhiệt độ dự báo ở Thủ đô Hà Nội ngày 25/5/2023.
|
t(h) |
10 |
11 |
12 |
13 |
|
T(0C) |
32 |
33 |
34 |
34 |
Ta có nhiệt độ T là hàm số của thời điểm t vì mỗi giá trị của t chỉ xác định đúng một giá trị của T.
Ngược lại, thời điểm t không phải là hàm số của nhiệt độ T, vì nhiệt độ T = 340C tương ứng với hai thời điểm khác nhau t = 12 và t = 13.
Chú ý: Khi y là hàm số của x, ta viết \(y = f(x);y = g(x),...\)
Ví dụ: Cho hàm số y = f(x) = x + 3.
f(-2) = -2 + 3 = 1; f(0) = 0 + 3 = 3
2. Mặt phẳng tọa độ
Khái niệm: Mặt phẳng có hệ trục tọa độ Oxy gọi là mặt phẳng tọa độ.
- Ox nằm ngang gọi là trục hoành;
- Oy thẳng đứng gọi là trục tung;
- O gọi là gốc tọa độ.
Tọa độ của một điểm:
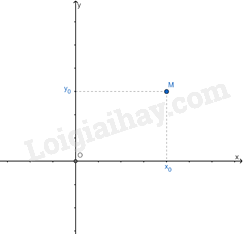
Trong mặt phẳng tọa độ, mỗi điểm M xác định duy nhất một cặp số \(({x_0};{y_0})\) và mỗi cặp số \(({x_0};{y_0})\) xác định duy nhất một điểm M.
Cặp số \(({x_0};{y_0})\) gọi là tọa độ của M, kí hiệu là M(x0,y0), trong đó x0 là hoành độ, y0 là tung độ của điểm M.
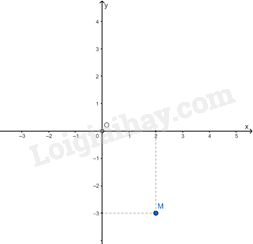
Ví dụ: Điểm M có tọa độ là (2; -3), kí hiệu là M(2; -3). Số 2 gọi là hoành độ, số -3 gọi là tung độ của điểm M.
3. Đồ thị của hàm số
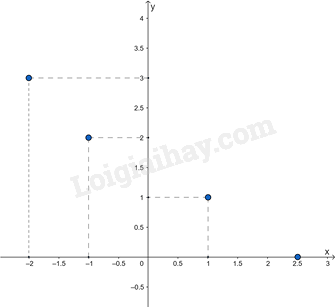
Đồ thị của hàm số y = f(x) là tập hợp tất cả các điểm biểu diễn các cặp giá trị tương ứng (x; y) trên mặt phẳng tọa độ.
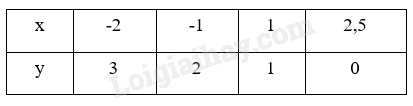
Ví dụ: Đồ thị của hàm số y = f(x) cho bởi bảng:
Search google: "từ khóa + timdapan.com" Ví dụ: "Lý thuyết Khái niệm hàm số và đồ thị của hàm số SGK Toán 8 - Kết nối tri thức timdapan.com"







