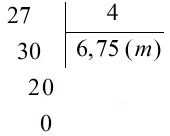Lý thuyết chia một số tự nhiên cho một số tự nhiên mà thương tìm được là một số thập phân

a) Ví dụ 1: Một cái sân hình vuông có chu vi 27m. Hỏi cạnh của sân dài bao nhiêu mét?

Ta phải thực hiện phép chia:       \(27 : 4 = \; ?\)

Thông thường ta đặt tính rồi làm như sau:

•  \(27\) chia \(4\) được \(6\), viết \(6\);

    \(6\) nhân \(4\) được \(24\), \(27\) trừ \(24\) được \(3\), viết \(3\);

•  Để chia tiếp, ta viết dấu phẩy vào bên phải \(6\) và viết thêm chữ số \(0\) vào bên phải \(3\) được \(30\).

   \(30\) chia \(4\) được \(7\), viết \(7\); 

   \(7\) nhân \(4\) bằng \(28\); \(30\) trừ \(28\) bằng \(2\), viết \(2\).

•  Viết thêm chữ số \(0\) vào bên phải \(2\) được \(20\); \(20\) chia \(4\) được \(5\) viết \(5\);

    \(5\) nhân \(4\) bằng \(20\); \(20\) trừ \(20\) bằng \(0\) viết \(0\).

Vậy:     \( 27 : 4 = 6,75 \;(m)\).

b) Ví dụ 2:      \(43: 52 = \;?\)

Phép chia này có số bị chia \(43\) bé hơn số chia \(52\), ta có thể làm như sau:

• Chuyển \(43\) thành \(43,0\)

• Đặt tính rồi tính như phép chia \(43,0 : 52\) (chia số thập phân cho số tự nhiên).

Khi chia một số tự nhiên cho một số tự nhiên mà còn dư, ta tiếp tục chia như sau:

- Viết dấu phẩy vào bên phải số thương.

- Viết thêm vào bên phải số dư một chữ số 0 rồi chia tiếp.

- Nếu còn dư nữa, ta lại viết thêm bên phải số dư mới một chữ số 0 rồi tiếp tục chia, và có thể cứ làm như thế mãi.