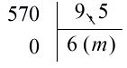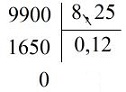Lý thuyết chia một số tự nhiên cho một số thập phân

a) Tính rồi so sánh kết quả tính:

    \(25 : 4\) và \((25 \times 5) : (4 \times 5)\)

    \(4,2 : 7\) và \( ( 4,2 \times 10) : (7 \times 10)\)

    \(37,8 : 9\) và \( (37,8 \times 100) : (9 \times 10)\)

Khi nhân số bị chia và số chia cùng một số khác \(0\) thì thương không thay đổi.

b) Ví dụ 1: Một mảnh vườn hình chữ nhật có diện tích \(57m^2\) , chiều dài \(9,5m\). Hỏi chiều rộng của mảnh vườn là bao nhiêu mét?

Ta phải thực hiện phép chia:       \(57 : 9,5 = \,?\; m\)

Ta có:       \(57 : 9,5 = (57 \times 10 ) : (9,5 \times 10)\)

                \(57 : 9,5 = 570 : 95\)

Thông thường ta đặt tính rồi làm như sau:

• Phần thập phân của số \(9,5\) có một chữ số.

• Viết thêm một chữ số \(0\) vào bên phải \(57\) (số bị chia) được \(570\); bỏ dấu phẩy ở số \(9,5\) được \(95\).

• Thực hiện phép chia \(570 : 95\).

Vậy:       \(5,7 : 9,5 = 6 \;(m)\).

c) Ví dụ 2:      \(99 : 8,25 = \;?\)

Ta đặt tính rồi làm như sau:

• Phần thập phân của \(8,25\) có hai chữ số.

• Viết thêm hai chữ số \(0\) vào bên phải \(99\) được \(9900\); bỏ dấu phẩy ở \(8,25\) được \(825\)

• Thực hiện phép chia \(9900: 825\). 

Muốn chia một số tự nhiên cho một số thập phân ta làm như sau:

- Đếm xem có bao nhiêu số thập phân ở phần thập phân của số chia thì viết thêm vào bên phải số bị chia bấy nhiêu chữ số \(0\).

- Bỏ dấu phẩy ở số chia rồi thực hiện phép chia như chia các số tự nhiên.