Hoạt động 7 trang 57 Tài liệu dạy – học Toán 9 tập 1
Giải bài tập Cho ba đường thẳng
Đề bài
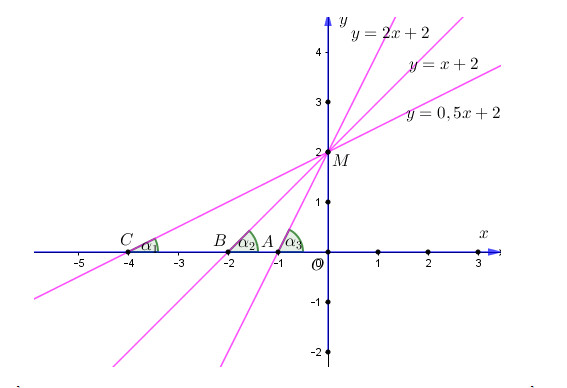
Cho ba đường thẳng \(\left( {{d_1}} \right):y = 0,5x + 2;\left( {{d_2}} \right):y = x + 2;\)\(\,\left( {{d_3}} \right):y = 2x + 2\) được vẽ trên cùng mặt phẳng tọa độ. Hãy xác định các góc \({\alpha _1},{\alpha _2},{\alpha _3}\) của \(\left( {{d_1}} \right),\left( {{d_2}} \right),\left( {{d_3}} \right)\) lần lượt với trục Ox. Sắp xếp theo thứ tự tăng dần ba góc vừa nêu.
Lời giải chi tiết
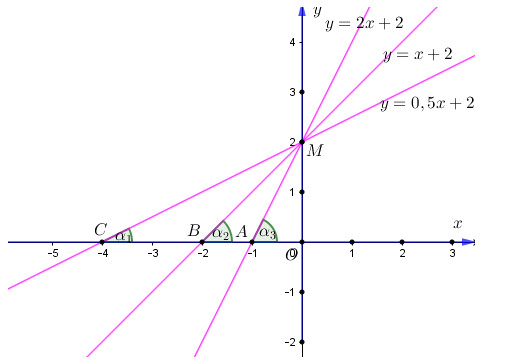
Đường thẳng \(y = 0,5x + 2\) cắt trục Ox tại điểm \(C\left( { - 4;0} \right)\) và đi qua điểm \(M\left( {0;2} \right)\) Khi đó ta có góc giữa đường thẳng \(y = 0,5x + 2\) và trục Ox chính là góc \(\widehat {MCx} = {\alpha _1}\) .
Đường thẳng \(y = x + 2\) cắt trục Ox tại điểm \(B\left( { - 2;0} \right)\) và đi qua điểm \(M\left( {0;2} \right)\) . Khi đó ta có góc giữa đường thẳng \(y = x + 2\) và trục Ox chính là góc \(\widehat {MBx} = {\alpha _2}\) .
Đường thẳng \(y = 2x + 2\) cắt trục Ox tại điểm \(A\left( { - 1;0} \right)\) và đi qua điểm \(M\left( {0;2} \right)\) . Khi đó ta có góc giữa đường thẳng \(y = 2x + 2\) và trục Ox chính là góc \(\widehat {MAx} = {\alpha _3}\) .
Khi đó ta có \({\alpha _1} < {\alpha _2} < {\alpha _3}\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Hoạt động 7 trang 57 Tài liệu dạy – học Toán 9 tập 1 timdapan.com"







