Hoạt động 3 trang 70 Tài liệu dạy – học Toán 9 tập 1

Đề bài

Xem hình 5 :

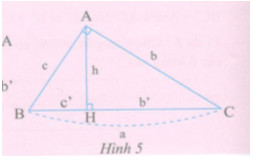
a) Hãy chứng tỏ hai tam giác AHB và CHA đồng dạng.

b) Lập tỉ số đồng dạng, từ đó tính h theo b’ và c’.

Lời giải chi tiết

a)

Có \(\widehat B + \widehat {BAH} = {90^o}\) (tam giác AHB vuông tại H)

\(\widehat B + \widehat C = {90^o}\) (tam giác ABC vuông tại A)

\( \Rightarrow \widehat {BAH} = \widehat C\)

Xét tam giác AHB và CHA có :

+) \( \widehat {BAH} = \widehat C\) (cmt);

+) \(\widehat {BHA} = \widehat {BAC} = {90^o}\)

\( \Rightarrow \)Tam giác AHB và CHA đồng dạng (g.g)

b)

Tam giác AHB và CHA đồng dạng

\( \Rightarrow \)\(\dfrac{{BH}}{{AH}} = \dfrac{{AH}}{{CH}} \Rightarrow A{H^2} = BH.CH\) hay \({h^2} = b'.c'\)