Bài 3. Điện thế, hiệu điện thế, tụ điện trang 75, 76, 77, 78, 79, 80, 81, 82, 83, 84 Vật Lí 11 Cánh diều

KĐ

Để dịch chuyển một điện tích dương đến gần điện tích dương khác, cần phải đẩy nó để thắng lực đẩy giữa chúng, Hình 3.1. Trong trường hợp này, ta nói rằng cần phải thực hiện một công để di chuyển một điện tích lại gần một điện tích khác.

Năng lượng của một điện tích di chuyển trong điện trường được xác định như thế nào?

Phương pháp giải:

Áp dụng kiến thức về công của lực điện để trả lời

Lời giải chi tiết:

Năng lượng của một điện tích di chuyển trong điện trường bằng công của lực điện tác dụng lên điện tích để di chuyển điện tích trong điện trường.

\({\rm{W}} = A = qEd\).

CH 1

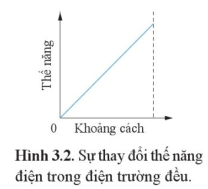
1. Vì sao đường biểu diễn sự thay đổi thế năng điện trong điện trường đều ở Hình 3.2 là một đường thẳng?

Phương pháp giải:

Đặc điểm của cường độ điện trường \(\vec E\) trong điện trường đều.

Lời giải chi tiết:

Trong điện trường đều, thế năng điện tại điểm M cách bản âm khoảng cách d là: \({{\rm{W}}_M} = A = qEd\). Do điện trường đều có \(\vec E\) không đổi nên thế năng\({{\rm{W}}_M}\) có dạng \({{\rm{W}}_M} = ad\)với a là hằng số, là hàm bậc nhất của khoảng cách d. Do đó, đồ thị biểu diễn mối liên hệ giữa thế năng và khoảng cách là một đường thẳng đi qua gốc tọa độ.

CH 2

2. Vì sao thế năng của điện tích tăng theo chiểu ngược với chiều của cường độ điện trường?

Phương pháp giải:

Giải thích bằng công của lực điện, định luật bảo toàn năng lượng.

Lời giải chi tiết:

Theo định luật bảo toàn năng lượng, công thực hiện để đưa một điện tích dương đến gần bản dương \(A = qEd > 0\) chuyển hóa thành thế năng điện của điện tích, làm thế năng tăng lên, nghĩa là, thế năng tăng khi đi từ bản âm đến bản dương. Trong khi đó, cường độ điện trường có chiều từ dương sang âm. Như vậy, thế năng của điện tích tăng theo chiểu ngược với chiều của cường độ điện trường.

CH 1

3. So sánh công của lực điện dịch chuyển một đơn vị điện tích dương từ điểm đang xét ra vô cực và công thực hiện để dịch chuyển một đơn vị điện tích dương từ vô cực về điểm đang xét

Phương pháp giải:

Công của lực điện \(A = qEd\).

Lời giải chi tiết:

Công của lực điện dịch chuyển một đơn vị điện tích dương từ điểm đang xét ra vô cực bằng công thực hiện để dịch chuyển một đơn vị điện tích dương từ vô cực về điểm đang xét nhưng trái dấu.

CH 2

4. Điện thế tại một điểm trong điện trường là gì?

Phương pháp giải:

Nêu định nghĩa của điện thế tại một điểm.

Lời giải chi tiết:

Điện thế tại một điểm trong điện trường là đại lượng vật lí đặc trưng cho điện trường tại điểm đó về thế năng, được các định bằng công của lực điện dịch chuyển một đơn vị điện tích dương từ điểm đang xét ra vô cực.

LT

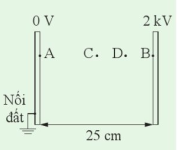
1. Cho hai bản cực song song, cách nhau 25 cm như Hình 3.3. Hiệu điện thế giữa hai bản là 2kV.

a) Hiệu điện thế giữa hai điểm A và B là bao nhiêu?

b) Cường độ điện trường tại C và tại D là bao nhiêu?

c) Tìm lực điện tác dụng lên một điện tích \( + 5\mu C\)đặt tại C.

Phương pháp giải:

Hiệu điện thế giữa A và B là hiệu điện thế giữa hai bản cực. Điện trường giữa hai bản là điện trường đều. Lực điện tác dụng lên điện tích đặt trong điện trường là \(\vec F = q\vec E\).

Lời giải chi tiết:

a) Hiệu điện thế giữa hai điểm A và B là \({U_{AB}} = 2kV\).

b) Điện trường giữa hai bản là điện trường đều nên cường độ điện trường tại C và tại D là bằng nhau và bằng: \(E = \frac{U}{d} = \frac{{2000}}{{0,25}} = 8000\)(V/m).

c) Lực điện tác dụng lên điện tích \( + 5\mu C\)đặt tại C là:

\(F = \left| q \right|E = {5.10^{ - 6}}.8000 = 0,04\)(N).

CH

5. Vì sao tụ điện có năng lượng?

Phương pháp giải:

Áp dụng định luật bảo toàn năng lượng.

Lời giải chi tiết:

Khi tụ điện chưa được tích điện (hiệu điện thế hai đầu tụ điện bằng 0), trên hai bản tụ điện không có điện tích.

Khi tụ điện được nối với nguồn điện, các bản tụ được tích điện. Đó là do nguồn điện thực hiện công đưa dần các điện tích đến các bản tụ điện. Theo định luật bảo toàn năng lượng, công này được đưa đến tụ điện, trở thành năng lượng tích lũy trong tụ điện. Vì thế, tụ điện có năng lượng.

LT

Một tụ điện có điện dung 2 000\(\mu F\)được tích điện đến 10 V. Tính năng lượng của tụ điện.

Phương pháp giải:

Sử dụng công thức tính năng lượng của tụ điện: \({\rm{W}} = \frac{{C{U^2}}}{2}\).

Lời giải chi tiết:

Điện dung của tụ \(C = 2000\mu F = {2.10^{ - 3}}F\). Hiệu điện thế hai đầu tụ \(U = 10V\).

Năng lượng của tụ điện là: \({\rm{W}} = \frac{{C{U^2}}}{2} = \frac{{({{2.10}^{ - 3}}){{.10}^2}}}{2} = 0,1\)(J).

VD

Cho các dụng cụ sau:

Một tụ điện có điện dung 100\(\mu F\)và hiệu điện thế định mức khoảng 12 V; 4 pin 1,5 V; một LED; một điện trở \(5\Omega \); công tắc, dây dẫn điện. Nêu phương án dùng các dụng cụ này chứng minh tụ điện có lưu trữ năng lượng.

Phương pháp giải:

Thiết kế sơ đồ mạch điện thể hiện cách mắc. Đầu tiên, tích điện cho tụ. Chứng minh tụ điện lưu trữ năng lượng bằng cách cho tụ giải phóng năng lượng qua LED để đèn sáng.

Lời giải chi tiết:

Ghép 4 pin lại tạo thành bộ nguồn có hiệu điện thế lớn hơn.

Mắc mạch điện như hình vẽ:

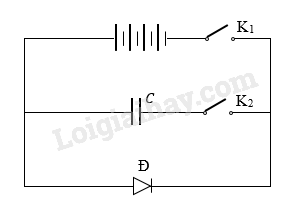
Đầu tiên, mở cả 2 khóa K₁ và K₂. Khi đó, tụ không được tích điện. Đóng khóa K₂, đèn LED không sáng.

Mở K₂, đóng K₁ để tích điện cho tụ. Sau một thời gian, tụ đã được tích điện, mở khóa K₁, tụ bị ngắt khỏi nguồn.

Đóng K₂, lúc này, đèn LED sáng một thời gian rồi tắt khi tụ phóng hết điện tích, chứng tỏ có năng lượng giải phóng từ tụ điện, nghĩa là trong quá trình tích điện, tụ đã lưu trữ năng lượng.

Bài 1

1. Quả cầu nhỏ thứ nhất mang điện tích \( - 0,1\mu C\), quả cầu nhỏ thứ hai mang điện tích có độ lớn \(0,05\mu C\). Hai quả cầu hút nhau với lực điện có độ lớn 0,05 N.

a) Điện tích của quả cầu thứ hai mang dấu gì?

b) Tính khoảng cách giữa hai tâm của hai quả cầu.

Phương pháp giải:

Sử dụng quy luật của lực điện tương tác giữa hai điện tích để xác định dấu điện tích. Áp dụng định luật Coulomb để suy ra khoảng cách giữa hai tâm quả cầu.

Lời giải chi tiết:

a) Hai quả cầu tác dụng lên nhau lực hút, do đó điện tích của hai quả cầu trái dấu nhau. Vậy quả cầu thứ hai tích điện dương.

b) Khoảng cách giữa hai tâm của hai quả cầu là: \(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}} \Rightarrow r = \sqrt {\frac{{k.\left| {{q_1}{q_2}} \right|}}{F}}  = \sqrt {\frac{{{{9.10}^9}.0,{{1.10}^{ - 6}}.0,{{05.10}^{ - 6}}}}{{0,05}}}  = 0,03\)(m) = 3 cm.

Bài 2

Đặt một điện tích thử dương \({q_1} = 2,{0.10^{ - 9}}\)C trong một điện trường thì điện trường tác dụng lên nó lực có độ lớn là \(F = 4,{0.10^{ - 9}}\)N.

Tìm độ lớn của cường độ điện trường tại vị trí đặt điện tích thử.

Phương pháp giải:

Sử dụng công thức tính độ lớn cường điện trường: \(E = \frac{F}{q}\).

Lời giải chi tiết:

Độ lớn của cường độ điện trường tại vị trí đặt điện tích thử là:

\(E = \frac{F}{q} = \frac{{4,{{0.10}^{ - 9}}}}{{2,{{0.10}^{ - 9}}}} = 2\)(V/m).

Bài 3

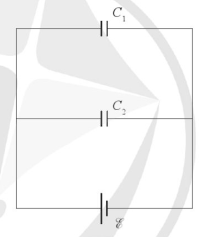
Hai tụ điện có điện dung lần lượt là \({C_1} = 100\mu F\); \({C_2} = 50\mu F\)và được mắc vào nguồn điện như hình vẽ. Biết hiệu điện thế giữa hai cực của nguồn điện là \(U = 12V\). Tính:

a) Điện dung của bộ tụ điện,

b) Hiệu điện thế giữa hai bản của mỗi tụ điện,

c) Điện tích của mỗi tụ điện.

Phương pháp giải:

Tính điện dung của bộ tụ song song \(C = {C_1} + {C_2}\). Hiệu điện thế của bộ tụ song song có đặc điểm gì? Tính điện tích của mỗi tụ điện bằng công thức \(Q = CU\).

Lời giải chi tiết:

Mạch gồm \({C_1}//{C_2}\)

a)      Điện dung của bộ tụ là: \(C = {C_1} + {C_2} = 100 + 50 = 150(\mu F)\).

b) Hiệu điện thế giữa hai bản của mỗi tụ điện bằng hiệu điện thế giữa hai cực của nguồn điện: \({U_1} = {U_2} = U = 12V\).

c) Điện tích của tụ điện C₁,C₂ lần lượt là:

\({Q_1} = {C_1}U = ({100.10^{ - 6}}).12 = 1,{2.10^{ - 3}}(C)\)

\({Q_2} = {C_2}U = ({50.10^{ - 6}}).12 = 0,{6.10^{ - 3}}(C)\).

Bài 4

Một đèn flash máy ảnh sử dụng tụ điện có điện dung \({C_1} = 4700\mu F\)và được sạc bằng pin 12 V. Sau đó, tụ điện được ngắt khỏi pin và phóng điện qua đèn để hiệu điện thế giữa hai bản tụ là 9,0 V. Tính năng lượng tụ điện đã chuyển qua đèn.

Phương pháp giải:

Tính năng lượng của tụ điện trước và sau khi phóng điện. Áp dụng định luật bảo toàn năng lượng, năng lượng tụ điện đã chuyển qua đèn bằng hiệu của năng lượng trước và sau khi phóng điện.

Lời giải chi tiết:

: Năng lượng của tụ điện trước khi phóng điện là: \({{\rm{W}}_1} = \frac{{C{U_1}^2}}{2} = \frac{{({{4700.10}^{ - 6}}){{.12}^2}}}{2} = 0,3384\) (J).

Năng lượng của tụ điện sau khi phóng điện là:

\({{\rm{W}}_2} = \frac{{C{U_2}^2}}{2} = \frac{{({{4700.10}^{ - 6}}){{.9}^2}}}{2} = 0,19035\)(J).

Năng lượng tụ điện đã chuyển qua đèn là:

\({\rm{W}} = {{\rm{W}}_1} - {{\rm{W}}_2} = 0,3384 - 0,19035 = 0,14805\)(J).