Bài tập chủ đề 1 trang 27 Vật Lí 10 Cánh diều

Phương pháp giải:

Sử dụng công thức: $v = \frac{s}{t}$

Lời giải chi tiết:

a)

Thời gian để ánh sáng từ Mặt Trời đến Trái Đất là:

$t = \frac{s}{v} = \frac{{{{150000000.10}^3}}}{{3,{{0.10}^8}}} = 500{\text{s}} = \frac{{25}}{3} \approx 8,33\left( {phut} \right)$

b)

Trái Đất quay quanh Mặt Trời 1 vòng hết 365 ngày = 8760 giờ

Tốc độ quay quanh Mặt Trời của Trái Đất là:

$v = \frac{s}{t} = \frac{{150000000.2\pi }}{{8760}} = 1,{076.10^5}\left( {km/h} \right)$

Đây là tốc độ trung bình, không phải là vận tốc của Trái Đất vì độ dịch chuyển của Trái Đất bằng 0.

Phương pháp giải:

- Sử dụng công thức tính quãng đường: s = v.t

- Sử dụng công thức tính độ dịch chuyển tổng hợp.

- Sử dụng công thức tính tốc độ trung bình và vận tốc trung bình.

Lời giải chi tiết:

a)

Quãng đường người đó đi về phía bắc là:

${s_2} = {v_2}.{t_2} = 60.\frac{{15}}{{60}} = 15\left( {km} \right)$

Tổng quãng đường đã đi là:

$s = {s_1} + {s_2} = 2,2 + 15 = 17,2\left( {km} \right)$

b)

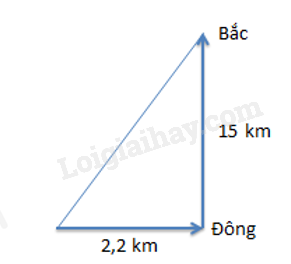
Độ lớn độ dịch chuyển tổng hợp là:

$d = \sqrt {d_1^2 + d_2^2}  = \sqrt {2,{2^2} + {{15}^2}}  = 15,16\left( {km} \right)$

c)

Thời gian người đó đi về phía đông là:

${t_1} = \frac{{{s_1}}}{{{v_1}}} = \frac{{2,{{2.10}^3}}}{{2,0}} = 1100(s) = 18,33\left( {phut} \right)$

Tổng thời gian đi của người này là:

$t = {t_1} + {t_2} = 18,33 + 15 = 33,33\left( {phut} \right)$

d)

Tốc độ trung bình là:

$v = \frac{{{s_1} + {s_2}}}{{{t_1} + {t_2}}} = \frac{{17,{{2.10}^3}}}{{33,33.60}} = 8,6\left( {m/s} \right)$

e)

Độ lớn của vận tốc trung bình là:

$v = \frac{d}{t} = \frac{{15,{{16.10}^3}}}{{33,33.60}} = 7,58\left( {m/s} \right)$

Phương pháp giải:

- Sử dụng kĩ năng vẽ đồ thị.

Lời giải chi tiết:

a)

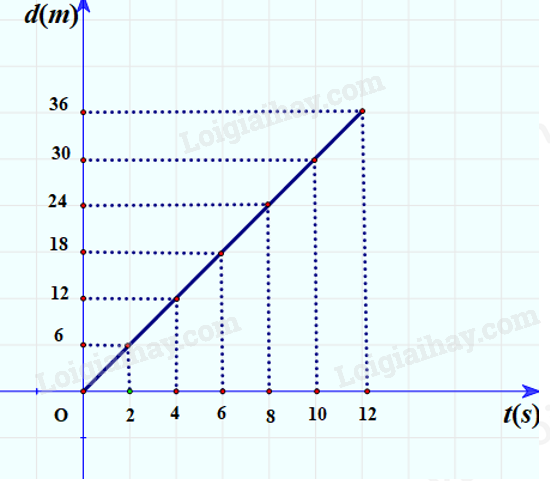
b)

- Từ t = 0,0 s đến t = 5,0 s người B đi được 10 m.

- Sau thời điểm t = 5,0 s người B đi với tốc độ không đổi là 4 m/s

+ Quãng đường người B đi được sau 1 s đi với tốc độ 4 m/s là: 10 + 4.1 = 14 m

+ Quãng đường người B đi được sau 2 s đi với tốc độ 4 m/s là: 10 + 4.2 = 18 m (đuổi kịp người A)

=> Người B đuổi kịp người A sau 2 s đi với tốc độ không đổi là 4m/s.

c)

Người B đi được 8 m trong khoảng thời gian đi với tốc độ không đổi (đến khi gặp nhau).