Bài 5. Tổng hợp và phân tích lực trang 65, 66, 67, 68, 69, 70 Vật Lí 10 Cánh diều
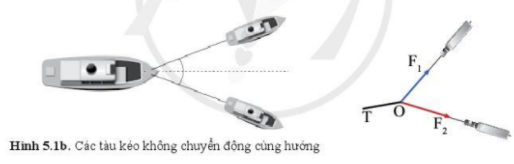
Ngày 23-3-2021, siêu tàu Ever Given (E-vơ Ghi-vòn), mang cờ Panama (Pa-na-ma), bị mắc. Biểu diễn quy tắc cộng vectơ cho trường hợp lực. Thảo luận, đề xuất phương án và thực hiện thí nghiệm tổng hợp hai lực đồng quy cùng phương. Xác định độ lớn và hướng của hợp lực F bằng cách dựng các vectơ lực P và lực Fđ đúng tỉ lệ. Thảo luận để thiết kế phương án thí nghiệm khác không cần sử dụng hệ thống ròng rọc và các quả cân. Có thể dùng lực kế đo trực tiếp các lực. Xác định hợp lực của hai tàu kéo trong
Câu hỏi tr 65
|
Ngày 23-3-2021, siêu tàu Ever Given (E-vơ Ghi-vòn), mang cờ Panama (Pa-na-ma), bị mắc cạn tại kênh đào Suez, làm tê liệt tuyến vận tải hàng hải quan trọng bậc nhất thế giới. Để giải cứu con tàu dài 400 m, rộng 59 m, chở 224 nghìn tấn hàng hóa, người ta đã phải huy động các tàu lai dắt để kéo mũi tàu Ever Given trở lại đường lưu thông qua kênh đào. Các tàu lai dắt không chuyển động cùng hướng nhưng hợp lực kéo của chúng vẫn giúp kéo mũi tàu Ever Given khỏi điểm mắc cạn. Vì sao như vậy? |
Lời giải chi tiết:
Các tàu lai dắt không chuyển động cùng hướng nhưng hợp lực kéo của chúng vẫn giúp kéo mũi tàu Ever Given khỏi điểm mắc cạn vì độ lớn của hợp lực bằng tổng độ lớn của lực của các tàu lai dắt và hướng thẳng về phía trước.
Câu hỏi tr 66
1. Quan sát, trả lời câu hỏi và thảo luận
| Biểu diễn quy tắc cộng vectơ cho trường hợp lực \({F_2}\) ngược chiều với lực \({F_1}\) khi \({F_1} > {F_2}\) và khi \({F_1} < {F_2}\). |
Phương pháp giải:
Sử dụng quy tắc tổng hợp hai lực cùng phương.
Lời giải chi tiết:
- TH1: \({F_1} > {F_2}\)

- TH2: \({F_1} < {F_2}\)

2. Quan sát, trả lời câu hỏi và thảo luận
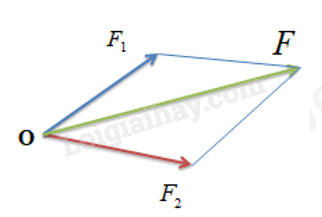
| Thảo luận, đề xuất phương án và thực hiện thí nghiệm tổng hợp hai lực đồng quy cùng phương. |
Phương pháp giải:
Thảo luận nhóm.
Lời giải chi tiết:
Phương án thí nghiệm:
- Dụng cụ: 2 lực kế, dây cao su
- Tiến hành:
+ Cho 2 lực kế cùng tác dụng vào 1 điểm đầu của sợi dây. Đầu kia cố định để làm dây biến dạng.
+ Biểu diễn hai vectơ F1, F2. Gốc tại điểm đặt tác dụng vào dây. Phương trùng với phương kéo 2 lực kế, hướng theo hướng kéo lực kế, độ lớn đọc số chỉ của lực kế.
+ Ghi lại kết quả bằng cách đánh dấu vị trí cuối dây dãn tới. Vị trí đầu là O, vị trí cuối là A.
+ Thay 2 lực kế trên bằng 1 lực kế tác dụng vào đầu tự do của dây cao su sao cho dãn đúng bằng đoạn OA. Sau đó biểu diễn hợp lực bằng vectơ F. Ghi lại độ lớn, phương và chiều.
3. Quan sát, trả lời câu hỏi và thảo luận
| Xác định độ lớn và hướng của hợp lực F bằng cách dựng các vectơ lực P và lực Fđ đúng tỉ lệ. Đối chiếu với kết quả tính. |
Phương pháp giải:
Dựa và đặc điểm: phương, chiều, độ lớn của lực.
Lời giải chi tiết:
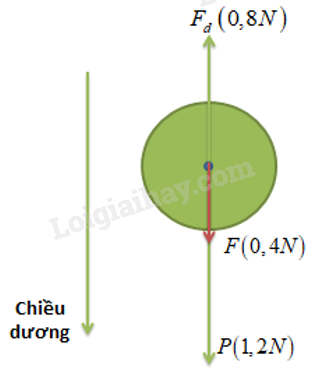
=> Trùng với kết quả tính được.
Câu hỏi tr 67
| Thảo luận để thiết kế phương án thí nghiệm khác không cần sử dụng hệ thống ròng rọc và các quả cân. Có thể dùng lực kế đo trực tiếp các lực. |
Phương pháp giải:
Thảo luận nhóm.
Lời giải chi tiết:
Phương án thí nghiệm:
Thay ròng rọc và các quả cân lần lượt bằng lực kế và dây cao su.
Tiến hành:
Dùng 3 lực kế. Hai lực kế gắn vào 2 đầu của sợi dây cao su và kéo căng. Lực kế còn lại treo vào giữa sợi dây cao su theo tỉ lệ 4:3.
Đọc số chỉ của mỗi lực kế.
Câu hỏi tr 68
|
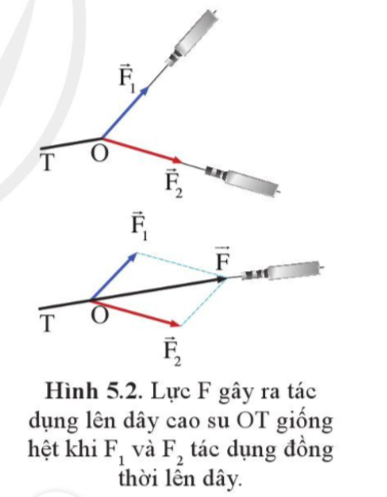
Xác định hợp lực của hai tàu kéo trong trường hợp mô tả ở hình 5.2. Coi độ lớn lực kéo của hai tàu như nhau, bằng 16.103 N và góc giữa hai lực kéo là 600.
|
Phương pháp giải:
Sử dụng lý thuyết hai lực tạo với nhau một góc bất kì.
Lời giải chi tiết:
Độ lớn hợp lực:
\(F = \sqrt {F_1^2 + F_2^2 + 2{F_1}.{F_2}.\cos \alpha } \)
\( \Rightarrow F = \sqrt {2.{{({{16.10}^3})}^2} + 2.{{\left( {{{16.10}^3}} \right)}^2}.\cos {{60}^0}} \)
\( \Rightarrow F = 27713\left( N \right)\)
Câu hỏi tr 70
| Hãy chứng tỏ rằng trong trường hợp con nhện ở trên, lực T cân bằng với hợp lực của P và Fđ. |
Phương pháp giải:
Sử dụng lý thuyết phân tích lực.
Lời giải chi tiết:
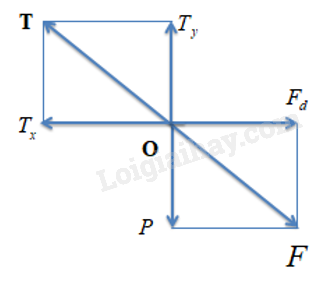
Phân tích lực căng T thành 2 thành phần \({T_x}\) và \({T_y}\)
Ta có: \(\widehat {{T_x}O{T_y}} = \widehat {{F_d}OP} = {90^0}\)
Con nhện nằm yên tại O => T cân bằng với F.
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 5. Tổng hợp và phân tích lực trang 65, 66, 67, 68, 69, 70 Vật Lí 10 Cánh diều timdapan.com"