Bài 21. Động lực học của chuyển động tròn. Lực hướng tâm trang 131, 132, 133, 134 Vật Lí 10 Chân trời sáng tạo
Trong hệ Mặt Trời, chuyển động của một số hành tinh như Trái Đất được xem gần đúng là chuyển động tròn đều xung quanh Mặt Trời (Hình 21.3). Vinasat-1 là vệ tinh viễn thông địa tĩnh (có vị trí cố định trong không gian so với Trái Đất) đầu tiên của Việt Nam được phóng vào vũ trụ năm 2008. Khi ô tô chạy theo đường vong cung, tài xế cần lưu ý những điều gì để tránh tai nạn xảy ra? Cho bán kính cung tròn mà xe chạy theo bằng 35,0 m, hệ số ma sát nghỉ giữa mặt đường và bánh xe bằng 0,523. Xác định tốc
CH 1
|
1. Trong hệ Mặt Trời, chuyển động của một số hành tinh như Trái Đất được xem gần đúng là chuyển động tròn đều xung quanh Mặt Trời (Hình 21.3). Lực nào đóng vai trò là lực hướng tâm trong chuyển động này của Trái Đất.
|
Lời giải chi tiết:
Lực đóng vai trò là lực hướng tâm trong chuyển động này là trọng lực (lực hấp dẫn).
LT
|
Vinasat-1 là vệ tinh viễn thông địa tĩnh (có vị trí cố định trong không gian so với Trái Đất) đầu tiên của Việt Nam được phóng vào vũ trụ năm 2008. Biết khối lượng vệ tinh là m = 2,7 tấn và vệ tinh có quỹ đạo chuyển động nằm trong mặt phẳng xích đạo cách tâm Trái Đất 42 000 km. Hãy xác định độ lớn lực hướng tâm do Trái Đất tác dụng lên vệ tinh. |
Phương pháp giải:
Biểu thức tính lực hướng tâm: \({F_{ht}} = m.{a_{ht}} = m.\frac{{{v^2}}}{R}\)
Lời giải chi tiết:
Vệ tinh Vinasat-1 chuyển động trong mặt phẳng quỹ đạo với vận tốc là 9000 m/s
Ta có: m = 2,7 tấn = 2700 kg; R = 42 000 km = 4,2.107 m.
Lực hướng tâm do Trái Đất tác dụng lên vệ tinh là: \({F_{ht}} = m.\frac{{{v^2}}}{R} = 2700.\frac{{{{9000}^2}}}{{4,{{2.10}^7}}} \approx 5207(N)\)
CH 2
|
2. Khi ô tô chạy theo đường vong cung, tài xế cần lưu ý những điều gì để tránh tai nạn xảy ra? |
Phương pháp giải:
Vận dụng lí thuyết trong sách giáo khoa trang 132 – 133.
Lời giải chi tiết:
Khi ô tô chạy theo đường vòng cung, tài xế cần lưu ý: không được chạy tốc độ quá mức giới hạn với biểu thức tính tốc độ giới hạn là: \(v = \sqrt {\mu .g.R} \)
LT
|
Cho bán kính cung tròn mà xe chạy theo bằng 35,0 m, hệ số ma sát nghỉ giữa mặt đường và bánh xe bằng 0,523. Xác định tốc độ tối đa để xe có thể đi vào đoạn đường cung tròn an toàn. |
Phương pháp giải:
Tốc độ giới hạn của xe khi đi trong đoạn đường cung tròn: \(v = \sqrt {\mu .g.R} \)
Lời giải chi tiết:
Ta có: \(\mu = 0,523\); R = 35,0 m; g = 10 m/s2
=> Tốc độ giới hạn của xe là: \(v = \sqrt {\mu .g.R} = \sqrt {0,523.10.35} \approx 13,53(m/s)\)
VD
|
Khi xe chạy theo đường vòng cung nằm ngang, tốc độ tối đa của xe để giữ an toàn phụ thuộc vào hệ số ma sát nghỉ và bán kính đường tròn? Tốc độ này có phụ thuộc vào trọng lượng của xe không? Từ đó, hãy đề xuất những yếu tố quan trọng cần lưu ý khi thiết kế cầu đường có hình vòng cung. |
Phương pháp giải:
Biểu thức tính tốc độ giới hạn khi xe chạy theo đường vòng cung: \(v = \sqrt {\mu .g.R} \)
Lời giải chi tiết:
Dựa vào biểu thức tính tốc độ giới hạn của xe chạy theo đường vòng cung, ta có tốc độ tối đa của xe để giữ an toàn tỉ lệ thuận với căn bậc 2 của hệ số ma sát nghỉ và bán kính đường tròn
Tốc độ này không phụ thuộc vào trọng lượng của xe.
=> Những yếu tố quan trọng cần lưu ý khi thiết kế cầu đường có hình vòng cung:
+ Mặt đường phải nghiêng một góc θ so với phương ngang để hợp lực hướng vào tâm đường tròn và đóng vai trò là lực hướng tâm.
BT 1
|
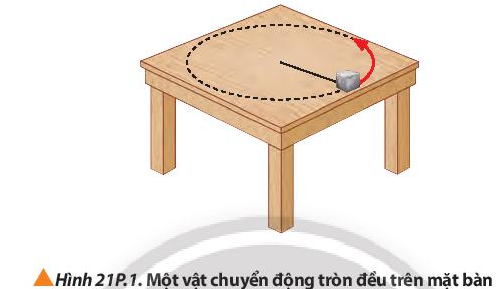
1. Một đầu của dây nhẹ dài 0,80 m được buộc một vật có khối lượng 3,00 kg. Vật chuyển động tròn đều quanh đầu kia của dây trên mặt bàn nằm ngang (Hình 21P.1). Giả sử không có ma sát giữa vật và mặt bàn. Khi tốc độ quay của dây là 1,60 vòng/s thì dây đứt. Tính lực căng dây lớn nhất.
|
Phương pháp giải:
Biểu thức tính lực hướng tâm: \({F_{ht}} = m.{a_{ht}} = m.{\omega ^2}.R\)
Lời giải chi tiết:
Ta có lực căng dây đóng vai trò là lực hướng tâm
Do khối lượng và bán kính của vật chuyển động xung quanh bàn không đổi nên lực căng phụ thuộc vào tốc độ góc. Lực căng dây lớn nhất khi tốc độ góc lớn nhất
Ta có: m = 3 kg; R = 0,8 m; \({\omega _{\max }}\)= 1,6 vòng/s = 1,6.2π = 10 rad/s.
=> Lực căng dây lớn nhất là: \({T_{\max }} = {F_{ht\max }} = m.\omega _{\max }^2.R = {3.10^2}.0,8 = 240(N)\).
BT 2
|
2. Mô hình đơn giản của nguyên tử hydrogen giả sử rằng electron chuyển động tròn đều quanh hạt nhân với tốc độ bằng 2,2.106 m/s. Quỹ đạo chuyển động có bán kính bằng 0,53.10-10 m. Hãy tính độ lớn của lực tương tác giữa electron và hạt nhân. |
Phương pháp giải:
Biểu thức tính lực hướng tâm: \({F_{ht}} = m.{a_{ht}} = m.\frac{{{v^2}}}{R}\)
Lời giải chi tiết:
Lực tương tác giữa các electron và hạt nhân đóng vai trò là lực hướng tâm.
Ta có me = 9,1.10-31 kg; v = 2,2.106 m/s; R = 0,53.10-10 m.
=> Độ lớn lực hướng tâm:
\({F_{ht}} = m.\frac{{{v^2}}}{R} = 9,{1.10^{ - 31}}.\frac{{{{(2,{{2.10}^6})}^2}}}{{0,{{53.10}^{ - 10}}}} \approx 8,{31.10^{ - 7}}(N)\)
BT 3
|
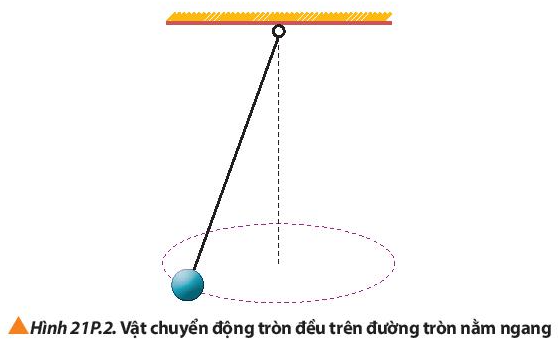
3. Một vật nặng có kích thước nhỏ, có khối lượng 0,50 kg, được buộc vào đầu một dây có chiều dài 1,5 m. Vật chuyển động đều trên đường tròn nằm ngang (Hình 21P.2). Cho biết dây chỉ chịu được lực căng tối đa bằng 50 N. Hãy tính tốc độ quay lớn nhất của vật để dây không bị đứt.
|
Phương pháp giải:
Biểu thức tính lực hướng tâm: \({F_{ht}} = m.{a_{ht}} = m.\frac{{{v^2}}}{R}\)
Lời giải chi tiết:
Lực đóng vai trò là lực hướng tâm trong trường hợp trên là lực căng.
=> Vận tốc cực đại của vật để dây không bị đứt là:
\(\begin{array}{l}{T_{\max }} = {F_{ht\max }} = m.\frac{{v_{\max }^2}}{R}\\ \Rightarrow {v_{\max }} = \sqrt {\frac{{{T_{\max }}.R}}{m}} = \sqrt {\frac{{50.1,5}}{{0,5}}} \approx 12,23(m/s)\end{array}\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 21. Động lực học của chuyển động tròn. Lực hướng tâm trang 131, 132, 133, 134 Vật Lí 10 Chân trời sáng tạo timdapan.com"