Bài 15. Năng lượng và ứng dụng của tụ điện trang 57, 58, 59 SBT Vật lí 11 Chân trời sáng tạo

Trắc nghiệm

15.1

Đề bài:

Năng lượng của tụ điện được xác định bởi công nào nào sau đây?

A. \(W = \frac{1}{2}Q{U^2}\)

B. \(W = \frac{1}{2}CU\)

C. \(W = C{U^2}\)

D. \(W = \frac{1}{2}\frac{{{Q^2}}}{C}\)

Phương pháp giải

Áp dụng lí thuyết năng lượng tụ điện

Lời giải chi tiết

Năng lượng tụ điện \(W = \frac{1}{2}\frac{{{Q^2}}}{C} = \frac{1}{2}C{U^2} = \frac{1}{2}QU\)

Đáp án D

15.2

Đề bài:

Trong các thiết bị sau, thiết bị nào không sử dụng tụ điện?

A. Máy khử rung tim.

B. Khối tách sóng trong máy thu thanh AM.

C. Pin dự phòng.

D. Tuabin nước.

Phương pháp giải

Vận dụng kiến thức thực tế

Lời giải chi tiết

Tuabin nước không có tụ điện.

Đáp án D

15.3

Đề bài:

Trên vỏ một tụ điện có ghi 20 pF – 200 V. Tụ điện tích trữ được năng lượng tối đa là

A. 4.10^-7 J.            

B. 8.10^-7 J.            

C. 4.10^-4 J.            

D. 4.10⁵ J.

Phương pháp giải

Áp dụng công thức tính năng lượng của tụ điện

Lời giải chi tiết

\(W = \frac{1}{2}C{U^2} = \frac{1}{2}{.20.10^{ - 12}}{.200^2} = {4.10^{ - 7}}{\rm{\;J}}\)

Đáp án A

15.4

Đề bài:

Với một tụ điện xác định, nếu hiệu điện thế giữa hai đầu tụ tăng 2 lần thì năng lượng điện trường của tụ

A. tăng 2 lần.                  

B. tăng 4 lần.                  

C. không đổi.                  

D. giảm 4 lần.

Phương pháp giải

Vận dụng mối quan hệ giữa năng lượng của tụ điện và hiệu điện thế

Lời giải chi tiết

Với điện dung C xác định, năng lượng của tụ điện tỉ lệ với bình phương hiệu điện thế giữa hai bản tụ điện.

Đáp án B

15.5

Đề bài:

Xét các tụ điện giống nhau có điện dung C=20pF.  Ghép các tụ điện thành bộ tụ như Hình 15.1 và nối hai điểm M, N với nguồn điện có hiệu điện thế U = 12V. Điện tích của bộ tụ là

 

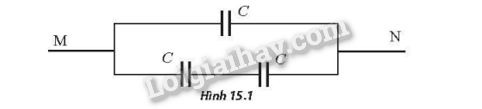
A. 720 pC.            

B. 360 pC.            

C. 160 pC.            

D. 240 pC.

Phương pháp giải

Sử dụng công thức ghép tụ điện

Lời giải chi tiết

Điện dung tương đương của bộ: \({C_{\rm{b}}} = C + \frac{C}{2} = \frac{3}{2}C = 30{\rm{pF}}\)

Điện tích của bộ tụ: \({Q_{\rm{b}}} = {C_{\rm{b}}}U = 30.12 = 360{\rm{pC}}\)

Đáp án B

15.6

Đề bài:

Trong một đèn flash chụp ảnh đơn giản, người ta sử dụng một tụ điện để có thể phát ra một chùm sáng với cường độ đủ lớn trong thời gian ngắn. Giả sử tụ điện được sử dụng có điện dung 0,20 F được sạc bằng pin 9,0 V, sau đó tụ phóng điện trong 0,001 s. Công suất phóng điện của tụ là

A. 8,1 W.              

B. 8100 W.           

C. 810 W.             

D. 81 W.

Phương pháp giải

Áp dụng công thức tính năng lượng và công suất của tụ điện

Lời giải chi tiết

Năng lượng của tụ điện: \(W = \frac{1}{2}C{U^2} = \frac{1}{2}.0,20.9,{0^2} = 8,1{\rm{\;J}}\)

Công suất phóng điện của tụ điện: \({\rm{P}} = \frac{W}{t} = \frac{{8,1}}{{0,001}} = 8100\;W\)

Đáp án B

---

Tự luận

15.1

Đề bài:

Đối với một tụ điện xác định, năng lượng của tụ điện phụ thuộc như thế nào vào hiệu điện thế giữa hai đầu của tụ điện?

Phương pháp giải

Vận dụng mối quan hệ giữa năng lượng của tụ điện và hiệu điện thế

Lời giải chi tiết

Đối với một tụ điện xác định thì điện dung của tụ điện sẽ không đổi, do đó năng lượng của tụ điện sẽ tỉ lệ bậc hai với hiệu điện thế đặt vào hai đầu của tụ điện.

\(W = \frac{1}{2}C{U^2}\)

15.2

Đề bài:

Đối với một tụ điện xác định, năng lượng của tụ điện giảm 9 lần khi điện tích của tụ điện thay đổi như thế nào?

Phương pháp giải

Vận dụng mối quan hệ giữa năng lượng của tụ điện và điện tích tụ điện

Lời giải chi tiết

Đối với một tụ điện xác định thì điện dung C của tụ điện là không đổi. Ta có công thức tính năng lượng của tụ điện: \(W = \frac{{{Q^2}}}{{2C}}\) , nên để năng lượng của tụ điện W giảm 9 lần thì điện tích của tụ điện Q phải giảm 3 lần.

15.3

Đề bài:

Cho một tụ điện có điện dung 3 pF được tích điện đến giá trị 9.10^-6 C. Tính năng lượng tích trữ trong tụ điện.

Phương pháp giải

Áp dụng công thức tính năng lượng của tụ điện

Lời giải chi tiết

Năng lượng tích trữ trong tụ điện là: \(W = \frac{{{Q^2}}}{{2C}} = \frac{{{{\left( {{{9.10}^{ - 6}}} \right)}^2}}}{{{{2.3.10}^{ - 12}}}} = 13,5{\rm{\;J}}\)

15.4

Đề bài:

Tính năng lượng tích trữ của tụ điện trong các trường hợp sau:

a) Một tụ điện 5000μF được gắn vào hai đầu một nguồn điện không đổi có hiệu điện thế 3 V.

b) Một tụ điện 5000μF được gắn vào hai đầu một nguồn điện không đổi có hiệu điện thế 230 V.

So sánh năng lượng tích trữ trong các trường hợp trên.

Phương pháp giải

Áp dụng công thức tính năng lượng của tụ điện

Lời giải chi tiết

a) Năng lượng tích trữ của tụ điện là: \(W = \frac{1}{2}C{U^2} = \frac{1}{2}{.5000.10^{ - 6}}{.3^2} = 0,0225{\rm{\;J}}\)

b) Năng lượng tích trữ của tụ điện là: \(W = \frac{1}{2}C{U^2} = \frac{1}{2}{.5000.10^{ - 6}}{.230^2} = 132,25{\rm{\;J}}\)

Vậy tụ điện 5000μF tích điện tới 230 V tích trữ nhiều năng lượng hơn.

15.5

Đề bài:

Đồ thị trong Hình 15.2 cho thấy sự phụ thuộc của U vào Q của một tụ điện.

 

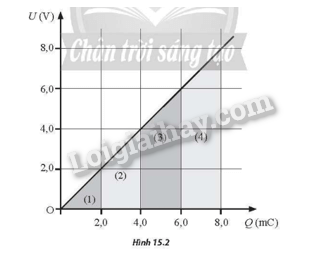
Vùng diện tích đầu tiên (1) (hình tam giác) hiển thị năng lượng tích trữ khi tụ điện được tích điện đến 2,0V. Năng lượng dự trữ khi đó là: \(W = \frac{1}{2}QU = \frac{1}{2}.2,{0.10^{ - 3}}.2,0 = {2.10^{ - 3}}{\rm{\;J}}\)

a) Tính điện dung C của tụ điện.

b) Hoàn thành Bảng 15.1 sau bằng cách tính diện tích của các vùng diện tích liên tiếp.

c) Vẽ đồ thị biểu diễn mối liên hệ giữa năng lượng dự trữ trong tụ W và hiệu điện thế giữa hai bản tụ U. Mô tả hình dạng của đồ thị này. Từ đó, hãy cho biết W phụ thuộc vào U như thế nào.

Phương pháp giải

Áp dụng công thức tính điện dung và điện tích của tụ điện

Lời giải chi tiết

a) Điện dung C của tụ điện là: \(C = \frac{Q}{U} = \frac{{2,0}}{{2,0}} = 1,0{\rm{mF}}\)

b)

Q (mC)	U (V)	Diện tích của vùng ΔW  (mJ)	Tổng diện tích W (mJ)
2,0	2,0	2,0	2,0
4,0	4,0	6,0	8,0
6,0	6,0	10,0	18,0
8,0	8,0	14,0	32,0

 

c) Đồ thị của W theo U có dạng parapol. Điều này cho thấy W phụ thuộc U theo tỉ lệ bậc hai.

 

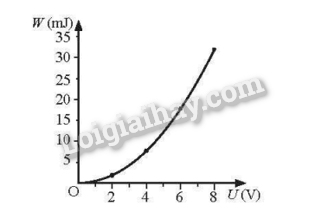
15.6

Đề bài:

Một tụ điện A có điện dung 0,6μF được gắn vào hai đầu một nguồn điện không đổi có hiệu điện thế 50 V. Sau đó, tụ được ngắt tụ ra khỏi nguồn và ghép song song với với một tụ điện B có điện dung 0,4μF chưa tích điện. Trong quá trình nối có một tia lửa điện nhỏ được phát ra. Hãy tính năng lượng của tia lửa điện phát ra khi nối hai tụ điện với nhau nếu giả sử toàn bộ lượng năng lượng mất mát trong quá trình ghép tụ được chuyển hoá thành năng lượng của tia lửa điện

Phương pháp giải

Áp dụng công thức tính năng lượng của tụ điện

Lời giải chi tiết

Năng lượng của tụ điện A trước khi được nối là: \(W = \frac{1}{2}{C_1}{U^2} = \frac{1}{2}.0,{6.10^{ - 6}}{.50^2} = 7,{5.10^{ - 4}}{\rm{\;J}}\)

Theo định luật bảo toàn điện tích, ta có: \(Q = {Q_1} + {Q_2} \Rightarrow {C_1}U = {C_1}U' + {C_2}U' \Rightarrow U' = \frac{{{C_1}U}}{{{C_1} + {C_2}}} = \frac{{0,{{6.10}^{ - 6}}.50}}{{0,{{6.10}^{ - 6}} + 0,{{4.10}^{ - 6}}}} = 30{\rm{\;V}}\)

Năng lượng của tụ điện A và B sau khi được nối là: \(W' = \frac{1}{2}{C_1}{U^{{\rm{'}}2}} + \frac{1}{2}{C_2}{U^{{\rm{'}}2}} = \frac{1}{2}.0,{6.10^{ - 6}}{.30^2} + \frac{1}{2}.0,{4.10^{ - 6}}{.30^2} = 4,{5.10^{ - 4}}{\rm{\;J}}\)

Năng lượng của tia lửa điện phát ra khi nối hai tụ điện với nhau là:

\({\rm{\Delta }}W = W - W' = 7,{5.10^{ - 4}} - 4,{5.10^{ - 4}} = {3.10^{ - 4}}{\rm{\;J}}\)

15.7

Đề bài:

Trên vỏ tụ điện (1) và (2) lần lượt ghi 4700μF − 35 V và 3300μF − 25 V. Tìm hiệu điện thế tối đa của bộ tụ điện khi ghép nối tiếp hai tụ này.

Phương pháp giải

Áp dụng công thức ghép tụ

Lời giải chi tiết

Để các tụ còn có thể hoạt động bình thường thì\(\left\{ {\begin{array}{*{20}{l}}{{U_1} \le {U_{{\rm{gh}}}}}\\{{U_2} \le {U_{{\rm{gh}}}}}\end{array}\left( * \right)} \right.\)

Khi ghép nối tiếp: \(\left\{ {\begin{array}{*{20}{l}}{U = {U_1} + {U_2}}\\{{C_1}{U_1} = {C_2}{U_2}}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{U_1} = \frac{{{C_2}}}{{{C_1} + {C_2}}}.U = \frac{{33}}{{80}}U}\\{{U_2} = \frac{{{C_1}}}{{{C_1} + {C_2}}}.U = \frac{{47}}{{80}}U}\end{array}} \right.} \right.\)

Kết hợp (*), ta được: \(\left\{ {\begin{array}{*{20}{l}}{\frac{{33}}{{80}}U \le 35V}\\{\frac{{47}}{{80}}U \le 25}\end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{l}}{U \le \frac{{2800}}{{33}}{\rm{\;V}} \approx 84,8{\rm{\;V}}}\\{U \le \frac{{2000}}{{47}}{\rm{\;V}} \approx 42,6{\rm{\;V}}}\end{array}} \right.\)

Vậy hiệu điện thế tối đa mà bộ tụ điện này còn hoạt động bình thường là 42,6 V.