Bài 1. Mô tả dao động trang 4, 5, 6, 7, 8 SBT Vật lí 11 Chân trời sáng tạo

Trắc nghiệm

1.1

Đề bài:

Chu kì dao động là:

A. Thời gian chuyển động của vật

B. Thời gian vật thực hiện được một dao động toàn phần

C. Số dao động toàn phần mà vật thực hiện được

D. Số dao động toàn phần mà vật thực hiện được trong một giây

Phương pháp giải:

Dựa vào lí thuyết về chu kì dao động

Lời giải chi tiết

Chu kì dao động là khoảng thời gian để vật thực hiện được một dao động toàn phần

Đáp án B

1.2

Đề bài:

Khi vật thực hiện được một dao động tương ứng với pha dao động sẽ thay đổi một lượng:

A. \(0rad\)

B. \(\frac{\pi }{2}rad\)

C. \(\pi rad\)

D. \(2\pi rad\)

Phương pháp giải:

Dựa vào lí thuyết về pha dao động

Lời giải chi tiết

Khi vật thực hiện được một dao động tương ứng với pha dao động sẽ thay đổi một lượng: 2π rad

Đáp án D

1.3

Đề bài:

Chu kì dao động của một vật được xác định bởi biểu thức

A. \(T = 2\pi \omega \)

B. \(T = \frac{{2\pi }}{\omega }\)

C. \(T = \pi \omega \)

D. \(T = \frac{\pi }{\omega }\)

Phương pháp giải:

Vận dụng lí thuyết về chu kì dao động

Lời giải chi tiết

Chu kì dao động của một vật được xác định bởi biểu thức:

\(T = \frac{{2\pi }}{\omega }\)

Đáp án B

1.4

Đề bài:

Đơn vị của tần số dao động trong hệ đơn vị SI là

A. Hz

B. s

C. cm

D. m

Phương pháp giải:

Vận dụng lí thuyết về tần số dao động

Lời giải chi tiết

Đơn vị của tần số dao động trong hệ đơn vị SI là Hz

Đáp án A

1.5

Đề bài:

Một vật đang dao động với chu kì là 0,3s tần số dao động của vật là

A. 0,3 Hz.

B. 0,33 Hz

C. 3,33 Hz.

D. 33 Hz.

Phương pháp giải:

Vận dụng công thức tính tần số dao động dựa vào chu kì: \(f = \frac{1}{T}\)

Lời giải chi tiết

Tần số dao động của vật là:

\(f = \frac{1}{T} = \frac{1}{{0,3}} = 3,33Hz\)

1.6

Đề bài:

Hai vật dao động điều hoà với biên độ dao động khác nhau nhưng có cùng tần số góc, khi đó ta có thể kết luận gì về pha của hai dao động?

A. Hai đao động cùng pha với nhau.

B. Hai dao động ngược pha với nhau

C. Hai dao động vuông pha với nhau

D. Chưa đủ dữ kiện để kết luận

Phương pháp giải:

Vận dụng lí thuyết về pha dao động

Lời giải chi tiết

Khi hai vật dao động điều hoà với cùng tần số góc, độ lệch pha giữa hai dao

động điều hoà không thay đổi theo thời gian nhưng đề bài chưa đủ dữ liệu để

xác định giá trị độ lệch pha.

Đáp án D

1.7

Đề bài:

Trong các dao động đúng mô tả dưới đây, dao động này được xem là dao động tuần hoàn

A. Dao động của con lắc đồng hồ khi đang hoạt động.

B. Lao động của chiếc thuyền trên mặt sông

C. Dao động của quả bóng cao su đang này trên mặt đât.

D. Dao động của dây đàn sau khi được gãy

Phương pháp giải:

Vận dụng khái niệm dao động tuần hoàn: Sau những khoảng thời gian bằng nhau, vật trở lại vị trí cũ theo hướng cũ thì dao động của vật đó là tuần hoàn

Lời giải chi tiết

Dao động của đồng hồ quả lắc được xem như dao động tuần hoàn vì nó dao

động quanh một vị trí cân bằng xác định và chuyển động của nó được lặp lại

sau những khoảng thời gian bằng nhau.

Đáp án A

1.8

Đề bài:

Khi tiến hành thí nghiệm khảo sát vị trí vật nặng của con lắc là xo đang dao động bằng cách sử dụng thước thẳng, bạn học sinh thấy rằng vật nặng dao động từ vị trí 1 cm đến vị trí là 11 cm trên thước. Biên độ dao động của vật nặng trong con lắc lò xo là

A. 10 cm.

B. 6 cm.

C. 5 cm.

D. 12 cm.

Phương pháp giải:

Vận dụng công thức tính biên độ của vật \(A = \frac{{\left| {{x_2} - {x_1}} \right|}}{2}\)

Lời giải chi tiết

Biên độ dao động của vật nặng

\(A = \frac{{\left| {{x_2} - {x_1}} \right|}}{2} = \frac{{\left| {11 - 1} \right|}}{2} = 5cm\)

Đáp án C

1.9

Đề bài:

Một bạn học sinh quan sát thấy con lắc trong đồng hồ quả lắc thực hiện được 20 dao động trong 30 giây. Dao động của con lắc trong đồng hồ này có đặc điểm nào sau đây?

A. Dao động điều hòa, tần số là 1,5 Hz.

B. Dao động điều hoà, tần số là 0,7 Hz.

C. Dao động tuần hoàn, tần số là 1,5 Hz.

D. Dao động tuần hoàn, tần số là 0,7 Hz.

Phương pháp giải:

Vận dụng công thức tính tần số dao động: \(f = \frac{N}{t}\)

Lời giải chi tiết

Dao động của con lắc là dao động tuần hoàn có tần số

\(f = \frac{N}{t} = \frac{{20}}{{30}} = 0,7Hz\)

Đáp án D

1.10

Đề bài:

Các nhà thực nghiệm đo được tần số dao động của một hệ gồm thanh silicon siêu nhỏ có virus dính trên đó đang thực hiện dao động là 2,87.10¹⁴ Hz. Tần số góc của hệ dao động trên bằng bao nhiêu?

A. 1,89.10¹⁵ rad/s.

B. 3,48.10¹⁵ rad/s.

C. 2,18.10¹⁴ rad/s.

D. 4,57.10¹⁴ rad/s.

Phương pháp giải:

Vận dụng công thức tính tần số góc: \(\omega  = 2\pi f\)

Lời giải chi tiết

Tần số góc của hệ dao động

\(\omega  = 2\pi f = 2\pi .2,{87.10^{14}} = 1,{8.10^{15}}rad/s\)

1.11

Đề bài:

Hai vật dao động điều hoà có li độ được biểu diễn trên đồ thị li độ –thời gian như Hình 1.1. Phát biểu nào dưới đây mô tả đúng tính chất của hai vật?

 

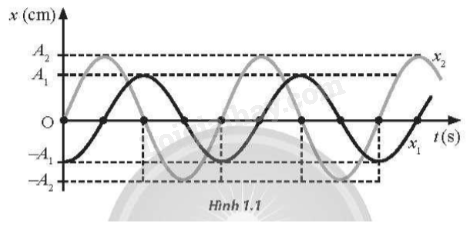
A. Hai vật dao động cùng tần số, cùng pha.

B. Hai vật dao động cùng tần số, vuông pha

C. Hai vật dao động khác tần số, cùng pha.

D. Hai vật dao động khác tần số, vuông pha

Phương pháp giải:

Dựa vào phương pháp đồ thị đọc đồ thị li độ theo thời gian

Lời giải chi tiết

Dựa vào trục Ot, ta thấy hai vật có cùng chu kì, nên hai vật có cùng tần số. Xét thời điểm ban đầu, vật 1 xuất phát từ vị trí cân bằng, vật 2 xuất phát từ biên âm, do đó hai vật dao động vuông pha nhau.

Đáp án B

---

Tự luận

1.1

Đề bài:

Có thể nói một vật đang dao động tuần hoàn thì cũng đang thực hiện dao động điều hoà không?

Phương pháp giải:

Vận dụng lí thuyết về dao động tuần hoàn và dao động điều hòa

Lời giải chi tiết

Không thể nói một vật đang dao động tuần hoàn thì cũng đang thực hiện dao động điều hoà vì vật được xem là thực hiện dao động điều hoà chỉ khi li độ của vật dao động là một hàm cosin (hoặc sin) theo thời gian.

1.2

Đề bài:

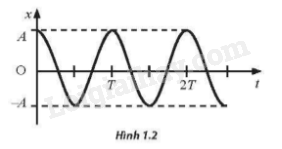
Đồ thị li độ – thời gian của một vật được thể hiện như Hình 1.2. Vật có đang thực hiện dao động điều hoà không? Vì sao?

 

Phương pháp giải:

Vận dụng lí thuyết về đồ thị của vật dao động điều hòa

Lời giải chi tiết

Vật đang thực hiện dao động điều hoà vì đồ thị li độ - thời gian của vật dao động có dạng hình sin.

1.3

Đề bài:

Một bạn học sinh cho rằng: “Một chiếc xích đu đang tự chuyển động qua lại thì đang thực hiện dao động tự do”. Nhận định này có hợp lí không?

Phương pháp giải:

Vận dụng lí thuyết về dao động tự do: Dao động của hệ xảy ra dưới tác dụng chỉ của nội lực được gọi là dao động tự do (dao động riêng)

Lời giải chi tiết

Nhận định trên không hợp lí vì xích đu có chịu tác dụng của ngoại lực như trọng lực, lực ma sát ở điểm treo, lực cản không khí, lực đẩy của gió,...

1.4

Đề bài:

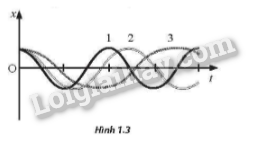
Hình 1.3 thể hiện đô thị li độ – thời gian của ba vật 1, 2 và 3 khác nhau đang thực hiện dao động điều hoà. Hãy so sánh chu kì dao động của ba vật.

 

Phương pháp giải:

Sử dụng phương pháp đồ thị

Lời giải chi tiết

Quan sát đồ thị, nhận thấy: T₃>T₂>T₁

1.5

Đề bài:

Trong phòng thí nghiệm, một bạn học sinh làm thí nghiệm với con lắc đơn và sử dụng một chiếc đồng hồ để bấm thời gian giữa hai lần liên tiếp quả nặng đi qua vị trí thấp nhất của quỹ đạo và ghi nhận được thời gian đó là 0,4 s. Từ đó, bạn học sinh kết luận “Chu kì dao động của con lắc đơn là 0,4s vì khoảng thời gian ngắn nhất để vật quay về vị trí cũ là 0,4 s”. Em có đồng ý với kết luận của bạn học sinh này không? Vì sao?

Phương pháp giải:

Vận dụng lí thuyết về chu kì dao động: Chu kì dao động là khoảng thời gian ngắn nhất để vật lặp lại trạng thái cũ (vị trí và vận tốc)

Lời giải chi tiết

Kết luận của bạn học sinh chưa chính xác vì chu kì dao động là khoảng thời gian ngắn nhất để vật lặp lại trạng thái cũ (vị trí và vận tốc). Tuy nhiên, khoảng thời gian bạn học sinh này đo được chỉ là khoảng thời gian ngắn nhất để quả nặng trở về vị trí cũ, còn vận tốc chưa lặp lại như cũ.

1.6

Đề bài:

Khi đến công viên một bạn học sinh nhìn thấy hai bạn nhỏ đang ngồi trên hai chiếc xích đu đung đưa qua lại và nhận thấy rằng khi xích đu của một bạn nhỏ lên tới vị trí cao nhất thì xích đu của bạn nhỏ còn lại luôn đi qua vị trí thấp nhất. Từ đó, bạn học sinh này cho rằng dao động của hai chiếc xích đu là dao động ngược pha. Theo em, nhận định của bạn học sinh này có hợp lí không? Vì sao?

Phương pháp giải:

Vận dụng lí thuyết về độ lệch pha giữa hai dao động

Lời giải chi tiết

Nhận định của bạn học sinh là không hợp lí vì khi một trong hai chiếc xích đu lên đến vị trí cao nhất (biên) thì xích đu còn lại qua vị trí thấp nhất (vị trí cân bằng), có nghĩa là dao động của hai chiếc xích đu là dao động vuông pha.

1.7

Đề bài:

Đồ thị li độ – thời gian của một vật dao động điều hoà được thể hiện như Hình 1.4. Dựa vào đồ thị, em hãy xác định:

 

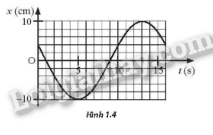
a) Biên độ dao động.

b) Chu kì dao động.

c) Tần số góc của dao động.

Phương pháp giải:

Sử dụng phương pháp đồ thị

Lời giải chi tiết

a. Biên độ dao động: A = 10cm

b. Chu kì dao động:  T = 16 s

c. Tần số góc của dao động

\(\omega  = \frac{{2\pi }}{T} = \frac{{2\pi }}{{16}} = \frac{\pi }{8}rad/s\)

1.8

Đề bài:

Khi ca sĩ hát, dây thanh quản của người ca sĩ sẽ dao động với tần số bằng với tần số của âm do người đó phát ra. Giả sử người ca sĩ hát âm “ Si giáng trưởng" có tần số khoảng 466 Hz thì dây thanh quán của người đó thực hiện được bao nhiêu dao động trong một giây.

Phương pháp giải:

Vận dụng lí thuyết về tần số dao động

Lời giải chi tiết

Tần số dao động của dây thanh quản bằng với tần số của âm do ca sĩ phát ra

f = 466 Hz

Vậy trong một giây thì dây thanh quản của ca sĩ thực hiện được 466 dao động.

1.9

Đề bài:

Một con lắc đơn dao động điều hoà trên Trái Đất với chu kì 1,60s. Nếu cho con lắc đơn này thực hiện dao động điều hoà trên Hỏa tinh thì chu kì con lắc đơn tăng lên 1,64 lần. Hỏi phải mất bao lâu để con lắc đơn thực hiện được 5 dao động trên Hỏa tinh.

Phương pháp giải:

Vận dụng công thức tính chu kì dao động

Lời giải chi tiết

Trên Hỏa tinh, con lắc đơn thực hiện dao động với chu kì là:

T = 1,64 . 1,60 = 2,624 s

Thời gian để con lắc đơn thực hiện được 5 dao động trên Hỏa tinh là:

 t = 5T = 5 . 2,624 = 13,12 s

1.10

Đề bài:

Một vật dao động điều hòa trên quỹ đạo dài 20 cm. Biết trong khoảng thời gian 90 s, vật thực hiện được 180 dao động. Tính biên độ, chu kì và tần số dao động của vật

Phương pháp giải:

Vận dụng công thức tính biên độ, chu kì dao động \(T = \frac{t}{N}\), tần số dao động \(f = \frac{1}{T}\)

Lời giải chi tiết

Vật chuyển động trên quỹ đạo dài 20 cm nên biên độ dao động là  

L = 2A = 20 cm => A = 10cm

Chu kì dao động: \(T = \frac{t}{N} = \frac{{90}}{{180}} = 0,5s\)

Tần số dao động của vật là: \(f = \frac{1}{T} = \frac{1}{{0,5}} = 2Hz\)

1.11

Đề bài:

Một vật đang thực hiện dao động điều hoà với tần số dao động 2 Hz. Tại thời điểm ban đầu, vật đang ở vị trí biên dương. Tính thời gian vật đến vị trí biên âm lần thứ 2023 kể từ lúc bắt đầu dao động.

Phương pháp giải:

Trong một chu kì dao động, vật đến vị trí biên âm một lần. Do đó, trong khoảng thời gian 2022T kể từ lúc bắt đầu dao động, vật qua vị trí biên âm 2022 lần và quay trở về vị trí biên dương. Thời gian để vật đi từ vị trí biên dương đến biên âm là 0,5 T.

Lời giải chi tiết

Chu kì dao động:  \(T = \frac{1}{f} = \frac{1}{2} = 0,5s\)

Trong một chu kì dao động, vật đến vị trí biên âm một lần. Do đó, trong khoảng thời gian 2022T kể từ lúc bắt đầu dao động, vật qua vị trí biên âm 2022 lần và quay trở về vị trí biên dương.

Thời gian để vật đi từ vị trí biên dương đến biên âm là 0,5 T.

Vậy thời gian để vật đến vị trí biên âm lần thứ 2023 kể từ lúc bắt đầu dao động là:

 Δt=2022T+0,5T=2022,5.0,5=1011,25 s

1.12

Đề bài:

Một vật đang thực hiện dao động điều hoà với biên độ 8 cm và chu kì dao động 0,5 s. Tại thời điểm ban đầu, vật đang ở vị trí biển âm. Tính tốc độ trung bình và độ lớn vận tốc trung bình của vật trong khoảng thời gian 2 s kể từ lúc bắt đầu dao động.

Phương pháp giải:

Vận dụng công thức tính tốc độ trung bình

Lời giải chi tiết

Ta có:  Δt = 2s = 4T

Quãng đường vật đi được trong một chu kì dao động là 4A.

Quãng đường vật đi được trong khoảng thời gian Δt là:  s =16 A

Tốc độ trung bình của vật trong khoảng thời gian 2 s kể từ lúc bắt đầu dao động là:

\({v_{tb}} = \frac{s}{{\Delta t}} = \frac{{16A}}{{4T}} = \frac{{128}}{2} = 64cm/s\)

Độ dịch chuyển của vật trong khoảng thời gian : d = ∆x = 0 cm

Độ lớn vận tốc trung bình của vật trong khoảng thời gian 2 s kể từ lúc bắt đầu dao động là: \(v{'_{tb}} = \frac{{\Delta x}}{{\Delta t}} = 0cm/s\) cm/s

1.13

Đề bài:

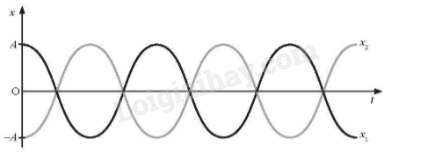
Cho hai vật thực hiện dao động điều hoà cùng biên độ, cùng tần số và dao động ngược pha với nhau. Biết tại thời điểm ban đầu vật 1 xuất phát từ biên dương. Hãy về phác đồ thị là độ – thời gian của hai vật dao động.

Phương pháp giải:

Sử dụng lí thuyết về phương trình li độ suy ra đồ thị li độ - thời gian

Lời giải chi tiết

Đồ thị là độ – thời gian của hai vật dao động được thể hiện như hình