Bài 32. Lực hướng tâm và gia tốc hướng tâm trang 60, 61, 62 SBT Vật lí 10 Kết nối tri thức với cuộc sống

32.1

Câu nào sau đây nói về gia tốc trong chuyền động tròn đều là sai?

A. Vectơ gia tốc luôn hướng vào tâm quỹ đạo.

B. Độ lớn của gia tốc a = \(\frac{{{v^2}}}{R}\), với v là tốc độ, R là bán kính quỹ đạo.

C. Gia tốc đặc trưng cho sự biến thiên về độ lớn của vận tốc.

D. Vectơ gia tốc luôn vuông góc với vectơ vận tốc ở mọi thời điểm.

Phương pháp giải:

Nắm được lý thuyết về gia tốc hướng tâm.

Lời giải chi tiết:

A đúng. Gia tốc của chuyển động tròn có phương, chiều luôn hướng vào tâm quỹ đạo của chuyển động tròn nên được gọi là gia tốc hướng tâm.

B đúng. a_ht = \(\frac{{{v^2}}}{r}\) với v là tốc độ, r là bán kính quỹ đạo.

C sai vì gia tốc hướng tâm đặc trưng cho sự biến thiên về hướng của vận tốc.

D đúng vì gia tốc hướng tâm luôn có chiều hướng vào tâm quỹ đạo còn vận tốc có phương trùng với tiếp tuyến đường tròn nên chúng luôn vuông góc với nhau.

Chọn đáp án C.

32.2

Phát biểu nào sau đây là đúng?

Trong chuyển động tròn đều

A. vectơ vận tốc luôn không đổi, do đó gia tốc bằng 0.

B. gia tốc hướng vào tâm quỹ đạo, độ lớn tỉ lệ nghịch với bình phương tốc độ.

C. phương, chiều và độ lớn của vận tốc luôn thay đổi.

D. gia tốc hướng vào tâm quỹ đạo, độ lớn tỉ lệ với bình phương tốc độ góc.

Phương pháp giải:

Nắm vững lý thuyết về các đặc điểm của chuyển động tròn đều.

Lời giải chi tiết:

A sai vì trong chuyển động tròn đều, độ lớn của vận tốc không đổi nhưng hướng luôn luôn thay đổi.

B sai vì độ lớn của gia tốc hướng tâm tỉ lệ thuận với bình phương tốc độ a_ht = \(\frac{{{v^2}}}{r}\).

C sai vì độ lớn của vận tốc không thay đổi chỉ có phương, chiểu thay đổi.

D đúng vì a_ht = \(\frac{{{v^2}}}{r}\)= ω²r.

Chọn đáp án D.

32.3

Một vật chuyển động theo đường tròn bán kính r = 100 cm với gia tốc hướng tâm a = 4 cm/s². Chu kì T của chuyển động vật đó là

A. 8π (s).               B. 6π (s).               C. 12π (s).             D. 10π (s).

Phương pháp giải:

Áp dụng công thức tính độ lớn của gia tốc hướng tâm:  a_ht = \(\frac{{{v^2}}}{r}\)= ω²r.

=> ω = \(\sqrt {\frac{{{a_{ht}}}}{r}} \).

Áp dụng công thức tính T = \(\frac{{2\pi }}{\omega }\).

Lời giải chi tiết:

Theo công thức tính độ lớn của gia tốc hướng tâm, ta có:  

a_ht = \(\frac{{{v^2}}}{r}\)= ω²r à ω = \(\sqrt {\frac{{{a_{ht}}}}{r}} \).

Chu kì T của chuyển động đó là: T = \(\frac{{2\pi }}{\omega }\)= 2π\(\sqrt {\frac{r}{{{a_{ht}}}}} \)= 2π\(\sqrt {\frac{{100}}{4}} \)= 10π (s).

Chọn đáp án D.

32.4

Một vệ tinh nhân tạo chuyển động tròn đều quanh Trái Đất, mỗi vòng hết 90 phút. Vệ tinh bay ở độ cao 320 km so với mặt đất. Biết bản của kinh Trái Đất là 6 380 km. Tốc độ và gia tốc hướng tâm của vệ tinh là

A. 7 792 m/s; 9,062 m/s².          B. 7651 m/s; 8,120 m/s².

C. 6 800 m/s; 7,892 m/s².           D. 7 902 m/s; 8,960 m/s².

Phương pháp giải:

Áp dụng công thức: ω = \(\frac{{2\pi }}{T}\) và a_ht = \(\frac{{{v^2}}}{r}\)= ω²r.

Lời giải chi tiết:

Theo đề có T = 90 ph = 90.60 = 5400 s

Khi đó ω = \(\frac{{2\pi }}{T}\) = \(\frac{{2\pi }}{{5400}}\) (rad/s).

Gia tốc hướng tâm của vệ tinh là:

a_ht = \(\frac{{{v^2}}}{r}\)= ω²r = \({\left( {\frac{{2\pi }}{{5400}}} \right)^2}.({6380.10^3} + {320.10^3})\)≈ 9,062 m/s².

Chọn đáp án A.

32.5

Một vật khối lượng m đang chuyển động tròn đều trên một quỹ đạo bán kính r với tốc độ góc ω. Lực hướng tâm tác dụng vào vật là:

A. F_ht = mω²r.        B. F_ht = \(\frac{{mr}}{\omega }\).                 C. F_ht = rω².              D. F_ht = mω².

Phương pháp giải:

Theo định luật II Newton: F = ma.

Tính gia tốc hướng tâm a_ht = \(\frac{{{v^2}}}{r}\)= ω²r.

Lời giải chi tiết:

Theo định luật II Newton: F_ht = ma_ht

Mà gia tốc hướng tâm a_ht = \(\frac{{{v^2}}}{r}\)= ω²r.

=> F_ht = mω²r.

Chọn đáp án A.

32.6

Một vật đang chuyển động tròn đều dưới tác dụng của lực hướng tâm F, Nếu tăng bán kính quỹ đạo gấp hai lần so với trước và đồng thời giảm tốc độ còn một nửa thì so với ban đầu, lực hướng tâm

A. giảm 8 lần.        B. giảm 4 lần.        C. giảm 2 lần.        D. không thay đổi.

Phương pháp giải:

Áp dụng công thức tính lực hướng tâm: F_ht = \(\frac{{m{v^2}}}{r}\)= mω²r.

Lời giải chi tiết:

Ta có: F_ht = \(\frac{{m{v^2}}}{r}\).

F_ht’ = \(\frac{{m{{(\frac{v}{2})}^2}}}{{2r}}\)= \(\frac{{m{v^2}}}{{8r}}\)= \(\frac{{{F_{ht}}}}{8}\).

Chọn đáp án A.

32.7

Một vật nhỏ khối lượng 150 g chuyển động tròn đều trên quỹ đạo bán kính 1,5 m với tốc độ 2 m/s. Độ lớn lực hướng tâm gây ra chuyền động tròn của vật là

A. 0,13 N.             B. 0,2 N.                C. 1,0 N.               D. 0,4 N.

Phương pháp giải:

Áp dụng công thức tính độ lớn lực hướng tâm: F_ht = \(\frac{{m{v^2}}}{r}\)= mω²r.

Lời giải chi tiết:

Độ lớn lực hướng tâm gây ra chuyền động tròn của vật là:

F_ht = \(\frac{{m{v^2}}}{r}\)= \(\frac{{0,{{15.2}^2}}}{{1,5}}\)= 0,4 N.

Chọn đáp án D.

32.8

Một vật chuyển động tròn đều với tốc độ là 3 m/s và có tốc độ góc là 10 rad/s. Tính gia tốc hướng tâm của vật đó.

Phương pháp giải:

Áp dụng công thức tính độ lớn của gia tốc hướng tâm:  a_ht = \(\frac{{{v^2}}}{r}\)= ω²r.

Lời giải chi tiết:

Ta có công thức liên hệ giũa tốc độ và tốc độ góc như sau: v = ωr => r = \(\frac{v}{\omega }\)

Gia tốc hướng tâm của vật là:

a_ht = \(\frac{{{v^2}}}{r}\)= ω²r = v.ω = 3.10 = 30 m/s².

32.9

Một chiếc xe đạp chạy với tốc độ 36 km/h trên một vòng đua có bán kính 100 m. Tính gia tốc hướng tâm của xe.

Phương pháp giải:

Áp dụng công thức tính độ lớn của gia tốc hướng tâm:  a_ht = \(\frac{{{v^2}}}{r}\)= ω²r.

Lời giải chi tiết:

Đổi v = 36 km/h = 10 m/s.

Gia tốc hướng tâm của xe là: a_ht = \(\frac{{{v^2}}}{r}\)= \(\frac{{{{10}^2}}}{{100}}\)= 1 m/s².

32.10

Một ô tô có khối lượng 4 tấn chuyển động qua một chiếc cầu vồng lên có bán kính cong 50 m với tốc độ 72 km/h. Lấy g = 10 m/s². Tính áp lực của ô tô nén lên cầu khi nó đi qua điểm cao nhất (giữa cầu).

Phương pháp giải:

Viết phương trình tổng hợp lực: \(\overrightarrow {{F_{ht}}}  = \overrightarrow P  + \overrightarrow N \).

Trong đó F_ht = \(\frac{{m{v^2}}}{r}\)= mω²r.

Lời giải chi tiết:

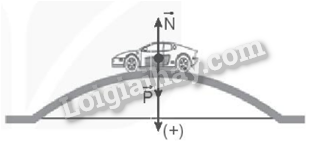
Đổi m = 4 tấn = 4000 kg; v = 72 km/h = 20 m/s.

Ta có hợp lực tác dụng lên ô tô: \(\overrightarrow {{F_{ht}}}  = \overrightarrow P  + \overrightarrow N \).

Chiếu lên phương hướng tâm: F_ht = P – N = \(\frac{{m{v^2}}}{r}\)

=> N = P - \(\frac{{m{v^2}}}{r}\) = mg - \(\frac{{m{v^2}}}{r}\)= 4000(10 - \(\frac{{{{20}^2}}}{{50}}\)) = 8000 N.

32.11

Một vật nhỏ khối lượng 200 g chuyển động tròn đều trên quỹ đạo bán kính 1 m. Biết trong 1 phút vật quay được 120 vòng. Tính độ lớn lực hướng tâm gây ra chuyển động tròn của vật.

Phương pháp giải:

Áp dụng công thức tính độ lớn lực hướng tâm: F_ht = \(\frac{{m{v^2}}}{r}\)= mω²r.

Lời giải chi tiết:

Đổi m = 200 g = 0,2 kg.

Theo đề có f = \(\frac{n}{t}\) = 120 vòng/ph = 2 vòng/s

=> ω = 2πf = 2π.2 = 4π (rad/s)

Độ lớn lực hướng tâm gây ra chuyển động tròn của vật là:

F_ht = mω²r = 0,2.(4π)².1 ≈ 31,6 N.

32.12

Ở độ cao bằng một nửa bán kính của Trái Đất có một vệ tinh nhân tạo chuyển động tròn đều xung quanh Trái Đất. Biết gia tốc rơi tự do ở mặt đất là g = 10 m/s² và gia tốc rơi tự do ở độ cao h so với mặt đất là g_h = \(\frac{{{R^2}}}{{{{(R + h)}^2}}}g\); bán kính của Trái Đất là 6 400 km. Tính tốc độ của vệ tinh.

Phương pháp giải:

Lực hấp dẫn đóng vai trò lực hướng tâm: F_hd = F_ht ó mg_h = \(\frac{{m{v^2}}}{{(R + h)}}\).

Lời giải chi tiết:

Theo đề ta có gia tốc rơi tự do ở độ cao h: g_h = \(\frac{{{R^2}}}{{{{(R + h)}^2}}}g\).

Lực hấp dẫn (trọng lực) đóng vai trò lực hướng tâm: F_hd = F_ht => mg_h = \(\frac{{m{v^2}}}{{(R + h)}}\).

=> \(\frac{{{R^2}}}{{{{(1,5R)}^2}}}g\)= \(\frac{{{v^2}}}{{1,5R}}\) è v = \(\sqrt {\frac{{gR}}{{1,5}}} \)= \(\sqrt {\frac{{{{10.6400.10}^3}}}{{1,5}}} \)≈ 6532 m/s.

Vậy tốc độ của vệ tinh là 6532 m/s.