Bài 26. Cơ năng và định luật bảo toàn cơ năng trang 48, 49, 50 SBT Vật lí 10 Kết nối tri thức với cuộc sống
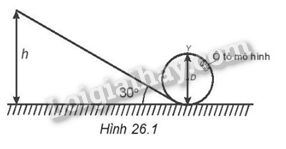
Một ô tô mô hình được thả nhẹ từ trạng thái nghỉ từ độ cao h của một cái rãnh không ma sát. Rãnh được uốn thành đường tròn có đường kính D ở phía cuối như trên Hình 26.1. Ô tô này trượt trên rãnh được cả vòng tròn mà không bị rơi. Giá trị tối thiểu của h là
26.1
Một ô tô mô hình được thả nhẹ từ trạng thái nghỉ từ độ cao h của một cái rãnh không ma sát. Rãnh được uốn thành đường tròn có đường kính D ở phía cuối như trên Hình 26.1. Ô tô này trượt trên rãnh được cả vòng tròn mà không bị rơi. Giá trị tối thiểu của h là
A. \(\frac{{5D}}{4}\). A. \(\frac{{3D}}{2}\). A. \(\frac{{5D}}{2}\). A. \(\frac{{5D}}{3}\).
Phương pháp giải:
Để ô tô này trượt trên rãnh được cả vòng tròn mà không bị rơi thì lực nén lên vòng tròn phải lớn hơn hoặc bằng 0.
Lời giải chi tiết:
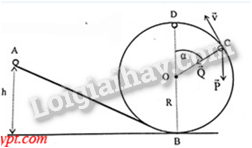
Chọn gốc thế năng tại điểm B như hình vẽ.
Áp dụng định luật bảo toàn cơ năng cho hai điểm A và C, ta có:
mgh = mgR(1 + cosα) + 0,5mv2 à v2 = 2gh – 2gR(1 + cosα)
Theo định luật II Newton, ta có: \(\overrightarrow Q + \overrightarrow P = m\overrightarrow a \)
Hay: Q + mgcosα = m\(\frac{{{v^2}}}{R}\)è Q = mg(\(\frac{{2h}}{R}\) - 2 – 3cosα) = N
Để ô tô có thể vượt qua hết vòng xiếc thì lực nén lên vòng tròn: Nmin ≥ 0
ó mg(\(\frac{{2h}}{R}\) - 5) ≥ 0 => h ≥ 2,5R ó h ≥ \(\frac{{5D}}{4}\).
Chọn đáp án A.
26.2
Một thùng gỗ được kéo trên đoạn đường nằm ngang dài 10 m bởi một lực kéo có độ lớn 80 N. Lực ma sát luôn ngược chiều chuyển động và có độ lớn 60 N. Độ tăng nội năng của hệ và độ tăng động năng của thùng gỗ lần lượt là
A. 200 J và 600 J. B. 200 J và 800 J.
C. 600 J và 200 J. D. 600 J và 800 J.
Phương pháp giải:
Nội năng của vật là tổng động năng và thế năng của các phân tử cấu tạo nên vật.
Nếu thế năng chuyển thành động năng thì lực sẽ sinh công phát động, ngược lại, khi động năng chuyển thành thế năng thì lực sinh công cản.
Áp dụng công thức tính công: A = F.s
Lời giải chi tiết:
Độ tăng nội năng của hệ là: ∆W = Acản = Fcản.s = 60.10 = 600 J.
Độ tăng động năng của thùng gỗ là: ∆Wđ = W - ∆W = 80.10 – 600 = 200 J.
Chọn đáp án C.
26.3
Năng lượng mà vật có được do vị trí của nó so với các vật khác được gọi là
A. động năng. B. cơ năng. C. thế năng. D. hoá năng.
Phương pháp giải:
Khái niệm về thế năng.
Lời giải chi tiết:
Thế năng của vật trong trường trọng lực là năng lượng lưu trữ trong vật do độ cao của vật so với gốc thế năng.
Chọn đáp án C.
26.4
Khi một quả bóng được ném lên thì
A. động năng chuyển thành thế năng.
B. thế năng chuyển thành động năng.
C. động năng chuyền thành cơ năng.
D. cơ năng chuyển thành động năng.
Phương pháp giải:
Vận dụng sư chuyển hóa giữa động năng và thế năng.
Lời giải chi tiết:
Động năng và thế năng có thể chuyển hóa qua lại lẫn nhau. Nếu thế năng chuyển thành động năng thì lực sẽ sinh công phát động, ngược lại, khi động năng chuyển thành thế năng thì lực sinh công cản.
Khi một quả bóng được ném lên thì động năng chuyển thành thế năng, lực sinh công cản.
Chọn đáp án A.
26.5
Dòng nước từ đỉnh thác có tốc độ là 5,1 m/s thì rơi tự do xuống chân thác.
Biết đình thác cao 5,7 m và lấy g = 9,8 m/s2. Với mỗi kg nước hãy tính
a) Động năng khi nước rơi từ đỉnh thác.
b) Thế năng ở đỉnh thác so với chân thác.
c) Tốc độ của nước khi đến chân thác.
Phương pháp giải:
a) Áp dụng công thức tính động năng: Wđ = \(\frac{1}{2}m{v^2}\).
b) Áp dụng công thức tính thế năng: Wt = mgh.
c) Áp dụng định luật bảo toàn cơ năng cho vị trí đỉnh thác và chân thác.
Wđỉnh = Wchân = \(\frac{1}{2}mv_{chan}^2\).
Lời giải chi tiết:
Chọn gốc thế năng tại chân thác.
a) Động năng khi nước rơi từ đỉnh thác là: Wđ = \(\frac{1}{2}m{v^2}\) = \(\frac{1}{2}.1.5,{1^2}\) ≈ 13 J.
b) Thế năng ở đỉnh thác so với chân thác là: Wt = mgh = 1.9,8.5,7 = 55,86 J.
c) Ta có cơ năng của dòng nước khi còn ở đỉnh thác là:
Wđỉnh = Wđ + Wt = 13 + 55,86 = 68,86 J.
Áp dụng định luật bảo toàn cơ năng cho vị trí đỉnh thác và chân thác.
Wđỉnh = Wchân = \(\frac{1}{2}mv_{chan}^2\) = 68,86 J.
è vchân ≈ 11,74 m/s.
Vậy tốc độ của nước khi đến chân thác là 11,74 m/s.
26.6
Một vận động viên nhào lộn thực hiện động tác nhảy từ mặt lưới bật ở độ cao 1,2 m so với mặt đất. Vận động viên này đạt độ cao 4,8 m rồi rơi trở xuống. Tìm vận tốc của vận động viên này khi rời bề mặt lưới bật. Lấy g = 9,8 m/s và bỏ qua sức cản của không khí.
Phương pháp giải:
Áp dụng định luật bảo toàn cơ năng.
Trong đó: W = Wđ + Wt = 0,5mv2 + mgh.
Lời giải chi tiết:
Chọn gốc thế năng tại mặt đất.
Cơ năng tại mặt lưới bật: W1 = \(\frac{1}{2}mv_1^2 + mg{h_1}\).
Cơ năng tại điểm cao nhất: W2 = mgh2.
Vì bỏ qua sức cản của không khí nên cơ năng được bảo toàn: W1 = W2.
ó \(\frac{1}{2}mv_1^2 + mg{h_1}\)= mgh2 ó \(\frac{1}{2}v_1^2\)+ 9,8.1,20 = 9,8.4,80 à v = 8,4 m/s.
Vậy vận tốc của vận động viên này khi rời bề mặt lưới bật là 8,4 m/s.
26.7
Vật nặng của một con lắc đơn được kéo lên đến độ cao 15 cm so với vị trí cân bằng rồi buông nhẹ. Trong suốt quá trình vật chuyển động, dây treo không bị co giãn. Bỏ qua mọi ma sát và khối lượng của dây treo. Lấy g = 9,8 m/s2. Tính vận tốc của vật nặng khi nó đi qua vị trí cân bằng.
Phương pháp giải:
Áp dụng định luật bảo toàn cơ năng.
Trong đó: W = Wđ + Wt = 0,5mv2 + mgh.
Lời giải chi tiết:
Chọn mốc thế năng là vị trí cân bằng.
Cơ năng của vật tại vị trí có độ cao 15 cm so với vị trí cân bằng là: W1 = mgh .
Cơ năng của vật tại vị trí cân bằng là: W2 = 0,5.mv2.
Vì bỏ qua mọi ma sát và khối lượng của dây treo, áp dụng định luật bảo toàn năng lượng ta được: W1 = W2 ó mgh = 0,5.mv2 ó gh = 0,5.v2
è v ≈ 1,71 m/s.
Vậy vận tốc của vật nặng khi nó đi qua vị trí cân bằng là 1,71 m/s.
26.8
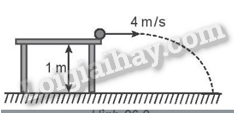
Một quả bóng nhỏ được ném với vận tốc ban đầu 4 m/s theo phương nằm ngang ra khỏi mặt bàn ở độ cao 1 m so với mặt sàn (Hình 26.2). Lấy g = 9,8 m/s2 và bỏ qua mọi ma sát. Tính vận tốc của quả bóng khi nó chạm mặt sàn.
Phương pháp giải:
Áp dụng định luật bảo toàn cơ năng.
Trong đó: W = Wđ + Wt = 0,5mv2 + mgh.
Lời giải chi tiết:
Chọn gốc thế năng tại mặt sàn.
Cơ năng của quả bóng trên mặt bàn là: W1 = \(\frac{1}{2}mv_1^2 + mg{h_1}\).
Cơ năng của quả bóng trên mặt sàn là: W2 = \(\frac{1}{2}mv_2^2\).
Vì bỏ qua mọi ma sát nên cơ năng được bảo toàn: W1 = W2.
ó \(\frac{1}{2}mv_1^2 + mg{h_1}\)= \(\frac{1}{2}mv_2^2\)ó \(\frac{1}{2}.m{.4^2}\)+ m.9,8.1 = \(\frac{1}{2}mv_2^2\)à v2 ≈ 5,97 m/s.
Vậy vận tốc của quả bóng khi nó chạm mặt sàn là 5,97 m/s.
26.9
Một vận động viên nhảy cầu thực hiện động tác bật nhảy để đạt độ cao 10 m so với mặt nước. Lấy g = 9,8 m/s2 và bỏ qua lực cản của không khí. Tìm vận tốc của vận động viên này khi chạm vào mặt nước.
Phương pháp giải:
Áp dụng định luật bảo toàn cơ năng.
Trong đó: W = Wđ + Wt = 0,5mv2 + mgh.
Lời giải chi tiết:
Chọn gốc thế năng tại mặt nước.
Cơ năng của vận động viên tại vị trí cách mặt nước 10 m: W1 = \(mgh\).
Cơ năng của vận động viên khi chạm mặt nước: W2 = \(\frac{1}{2}m{v^2}\)
Vì bỏ qua sức cản của không khí nên cơ năng được bảo toàn: W1 = W2.
ó \(mgh\)= \(\frac{1}{2}m{v^2}\) ó m.9,8.10 = 0,5.m.v2 à v = 14 m/s.
Vậy vận tốc của vận động viên này khi chạm vào mặt nước là 14 m/s.
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 26. Cơ năng và định luật bảo toàn cơ năng trang 48, 49, 50 SBT Vật lí 10 Kết nối tri thức với cuộc sống timdapan.com"







