Bài 13. Tổng hợp lực - Phân tích lực trang 40, 41, 42 SBT Vật lí 10 Chân trời sáng tạo

13.1

Khi có hai vecto lực \(\overrightarrow {{F_1}} ,\,\overrightarrow {{F_2}} \) đồng quy, tạo thành 2 cạnh của một hình bình hành thì vecto tổng hợp lực \(\overrightarrow F \) có thể

A. có điểm đặt tại 1 đỉnh bất kì của hình bình hành.

B. có phương trùng với đường chéo của hình bình hành.

C. có độ lớn F = F₁ + F₂.

D. cùng chiều với \(\overrightarrow {{F_1}} \)hoặc \(\overrightarrow {{F_2}} .\)

Phương pháp giải:

Vận dụng kiến thức về tổng hợp lực hai lực đồng quy.

Lời giải chi tiết:

Khi hai lực thành phần \(\overrightarrow {{F_1}} ,\,\overrightarrow {{F_2}} \) đồng quy, tạo thành 2 cạnh của một hình bình hành thì vecto tổng hợp lực \(\overrightarrow F \) được xác định bằng biểu thức: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}} \), hay chính là đường chéo của hình bình hành.

=> Chọn B

13.2

Hình vẽ nào sau đây biểu diễn đúng lực tổng hợp của hai lực \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \)?

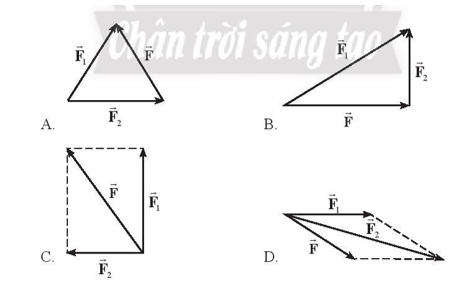
Phương pháp giải:

Vận dụng kiến thức về tổng hợp hai lực đồng quy.

Lời giải chi tiết:

Khi hai lực thành phần \(\overrightarrow {{F_1}} ,\,\overrightarrow {{F_2}} \) đồng quy, tạo thành 2 cạnh của một hình bình hành thì vecto tổng hợp lực \(\overrightarrow F \) được xác định bằng biểu thức: \(\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}} \), hay chính là đường chéo của hình bình hành.

=> Chọn C

13.3

Phát biểu nào sau đây về phép tổng hợp lực là sai?

A. Xét về mặt toán học, tổng hợp lực là phép cộng các vecto lực cùng tác dụng lên một vật.

B. Lực tổng hợp có thể xác định bằng quy tắc hình bình hành, quy tắc tam giác lực hoặc quy tắc đa giác lực.

C. Độ lớn của lực tổng hợp có thể lớn hơn, nhỏ hơn hoặc bằng tổng độ lớn của hai lực thành phần.

D. Lực tổng hợp là một lực thay thế các lực tác dụng đồng thời vào cùng một vật, có tác dụng tương đương các lực thành phần.

Phương pháp giải:

Vận dụng kiến thức về tổng hợp lực trên một mặt phẳng.

Lời giải chi tiết:

Độ lớn của lực tổng hợp chỉ có thể nhỏ hơn hoặc bằng tổng độ lớn của hai lực thành phần.

=> Chọn C

13.4

Hai lực \(\overrightarrow {{F_1}} ,\,\overrightarrow {{F_2}} \) song song cùng chiều, cách nhau một đoạn 20 cm. Độ lớn của lực \(\overrightarrow {{F_1}} \) là 24 N. Hỏi độ lớn của lực \(\overrightarrow {{F_2}} \) và điểm đặt của lực tổng hợp cách điểm đặt của lực \(\overrightarrow {{F_2}} \)một đoạn là bao nhiêu?

A. 6 N; 15 cm                                                 B. 42 N; 5 cm 

C. 6 N; 5 cm                                                    D. 42 N; 15 cm

Phương pháp giải:

Vận dụng kiến thức về tổng hợp hai lực song song cùng chiều.

Lời giải chi tiết:

\({F_2} = F - {F_1} = 6N.\)

\(\left\{ \begin{array}{l}\frac{{{d_2}}}{{{d_1}}} = \frac{3}{1}\\{d_2} + {d_1} = 20cm\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{d_1} = 5cm\\{d_2} = 15cm\end{array} \right.\)

=> Chọn A

13.1

Hai lực có giá đồng quy, vuông góc có độ lớn các lực thành phần là F₁ = 6 N và F₂ = 8 N (Hình 13.1). Xác định độ lớn của lực tổng hợp và góc hợp giữa vecto lực tổng hợp và vecto lực \(\overrightarrow {{F_1}} \).

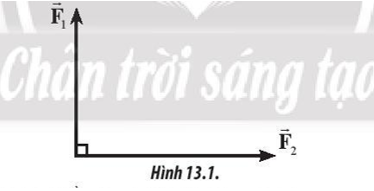
Phương pháp giải:

Vận dụng kiến thức về tổng hợp lực hai lực đồng quy.

Lời giải chi tiết:

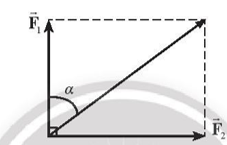
\(F = \sqrt {F_1^2 + F_2^2}  = 10N;\,\tan \alpha  = \frac{{{F_2}}}{{{F_1}}} = \frac{8}{6} \Rightarrow \alpha  \approx 53,{13^0}.\)

13.2

Đặt tại hai đầu thanh AB dài 60 cm hai lực song song cùng chiều và vuông góc với AB. Lực tổng hợp \(\overrightarrow F \) được xác định đặt tại O cách A một khoảng 15 cm và có độ lớn 12 N (Hình 13.2). Độ lớn của lực \(\overrightarrow {{F_1}} \) bằng bao nhiêu?

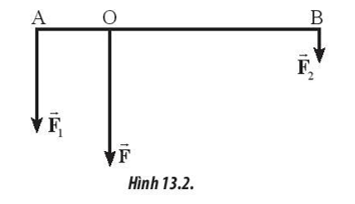
Phương pháp giải:

Vận dụng kiến thức về tổng hợp hai lực song song cùng chiều.

Lời giải chi tiết:

\(\frac{{{F_1}}}{{{F_2}}} = \frac{{{d_2}}}{{{d_1}}} \Rightarrow \frac{{{F_1}}}{{{F_2}}} = \frac{{45}}{{15}} = 3 \Rightarrow {F_1} - 3{F_2} = 0;\,{F_1} + {F_2} = 12.\)

Tìm được: F₁ = 9 N.

13.3

Một người đẩy máy cắt cỏ có khối lượng 15 kg di chuyển với một lực có độ lớn xem như không đổi bằng 80 N theo phương của giá đẩy như Hình 13.3. Biết góc tạo bởi giá đẩy và phương ngang là 45⁰.

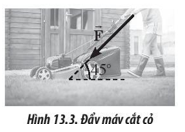
a) Tìm độ lớn của lực đẩy theo phương ngang và phương thẳng đứng.

b) Nếu từ trạng thái nghỉ, người này tác dụng lực để tăng tốc cho máy đạt tốc độ 1,2 m/s trong 3 s thì độ lớn lực ma sát trong giai đoạn này là bao nhiêu?

Phương pháp giải:

Vận dụng kiến thức về việc phân tích lực.

Lời giải chi tiết:

a) F_v = F.cos 45⁰ = 56,6 N; F_n = F.sin 45⁰ = 56,6 N

b) \(a = \frac{{1,2 - 0}}{3} = 0,4m/{s^2}.\)

F_ms = F_v – m.a = 56,6 -15.0,4 = 50,6 N.

13.4

Trò chơi “Xếp đá cân bằng” là môn nghệ thuật sao cho việc xếp những hòn đá lên nhau được cân bằng như Hình 13.4. Dưới góc nhìn Vật lí, em hãy cho biết nguyên nhân chính tạo nên sự cân bằng của hệ các viên đá.

Phương pháp giải:

Vận dụng kiến thức về tổng hợp hai lực song song cùng chiều.

Lời giải chi tiết:

Hợp lực của các lực: trọng lực của viên đá dài, trọng lực của các khối đá bên trái và bên phải của viên đá dài có phương đi qua điểm tiếp xúc giữa viên đá dài và hai viên đá đặt bên dưới.

13.5

Trong Hình 13.5, hai bạn nhỏ đang kéo một chiếc xe trượt tuyết. Xét lực kéo có độ lớn 45 N và góc hợp bởi dây kéo so với phương ngang là 40⁰.

a) Thành phần lực kéo theo phương ngang có độ lớn bao nhiêu?

b) Nếu xe trượt tuyết này chuyển động đều dưới tác dụng của lực kéo trên thì lực ma sát có độ lớn bao nhiêu?

Phương pháp giải:

Vận dụng kiến thức về việc phân tích lực.

Lời giải chi tiết:

a) F_v = F.cos 40⁰ = 34,5 N.

b) Vì xe được kéo thẳng đều nên: F_ms = F_v = 34,5 N.