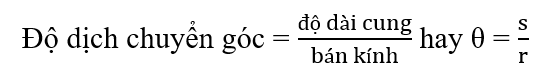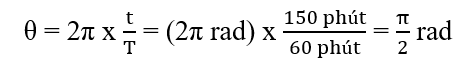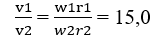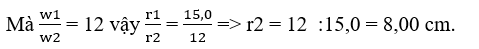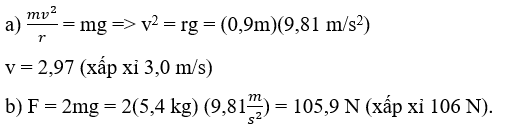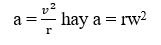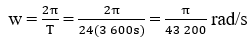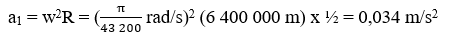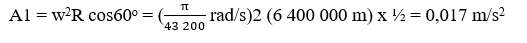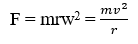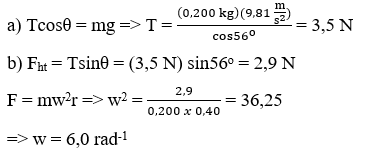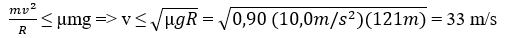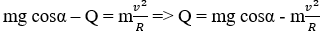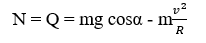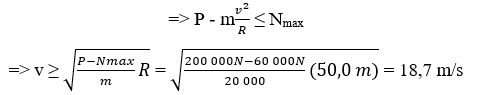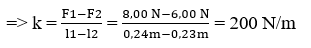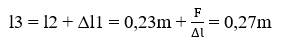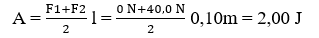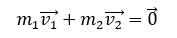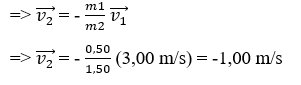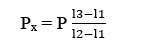Chủ đề 5. Chuyển động tròn và biến dạng trang 45, 46, 47 48, 49 SBT Vật Lí 10 Cánh diều

5.1

Phát biểu nào sau đây sai khi nói về một vật chuyển động tròn đều?

A. Quỹ đạo chuyển động là một đường tròn hoặc một phần của đường tròn

B. Tốc độ của vật không đổi theo thời gian

C. Với tốc độ xác định, bán kính quỹ đạo càng nhỏ thì phương của vận tốc biến đổi càng nhanh.

D. Với bán kính quỹ đạo xác định, nếu tốc độ tăng gấp đôi thì gia tốc hướng tâm cũng tăng gấp đôi.

Phương pháp giải:

Một vật chuyển động tròn đều:

• Quỹ đạo chuyển động là một đường tròn hoặc một phần của đường tròn
• Tốc độ của vật không đổi theo thời gian
• Với tốc độ xác định, bán kính quỹ đạo càng nhỏ thì phương của vận tốc biến đổi càng nhanh.

Lời giải chi tiết:

Đáp án D.

5.2

Một bánh xe đang quay đều, mỗi phút nó quay được 3 000 vòng. Phát biểu nào sau đây sai khi nói về chuyển động của bánh xe?

A. Độ dịch chuyển góc của một điểm bất kì trên bánh xe (trừ những điểm thuộc trục quay) trong khoảng thời gian 0,01 giây bằng π radian.

B. Những điểm cách trục quay 10,0 cm thì có tốc độ 10 π m/s

C. Hai điểm bất kì trên bánh xe nếu cách nhau 20,0 cm thì có tốc độ hơn kém nhau một lượng 20 π m/s.

D. Những điểm càng xa trục quay thì gia tốc hướng tâm càng lớn.

Lời giải chi tiết:

Đáp án C.

5.3

Biết kim phút của đồng hồ treo tường có chiều dài a = 10,0 cm

a) Tính tốc độ dịch chuyển góc và quãng đường đi của điểm đầu kim phút trong khoảng thời gian t = 15,0 phút

b) Biết tỉ số tốc độ của điểm đầu kim phút và tốc độ của điểm đầu kim giờ là 15,0. Tính chiều dài của kim giờ.

Phương pháp giải:

Góc θ ứng với cung tròn s mà vật đã đi được kể từ vị trí ban đầu gọi là độ dịch chuyển góc. Độ dịch chuyển góc được xác định bởi:

Lời giải chi tiết:

a) Độ dịch chuyển góc của kim phút là:

Quãng đường đi của điểm đầu kim phút là:

S = θr = 15,7 cm

b) Gọi tốc độ, tốc độ góc và chiều dài của kim phút và kim giờ lần lượt là v1, v2; w1, w2; r1, r2 theo giả thiết ta có:

5.4

Một người xách một xô có nước và vung tay làm xô nước quay trong mặt phẳng thẳng đứng, theo một vòng tròn đường kính 1,8 m. Biết khối lượng xô và nước là 5,4 kg.

a) Tính tốc độ nhỏ nhất mà xô nước phải được quay để khi ở đỉnh hình tròn, đáy xô quay lên trên, miệng hướng xuống dưới mà nước vẫn ở trong xô.

b) Giả sử tốc độ không đổi, lực tác dụng lên tay của người đó khi xô nước ở dưới cùng của đường tròn là bao nhiêu?

Lời giải chi tiết:

5.5

Coi Trái Đất là hình cầu có bán kính R = 6 400 km và quay quanh trục với chu kì 24,0 giờ. Tính gia tốc hướng tâm do Trái Đất chuyển động quay quanh trục gây ra cho một người đang đứng ở xích đạo và một người đứng ở vĩ tuyến 60,0^o.

Phương pháp giải:

Gia tốc hướng tâm có liên hệ với tốc độ v và bán kính quỹ đạo r theo công thức:

Lời giải chi tiết:

a) Tốc độ góc trong chuyển động quay của Trái đất là:

Gia tốc hướng tâm của người đứng ở xích đạo là:

Gia tốc hướng tâm của người ở vĩ tuyến 60^o là:

5.6

Ở hình 1,10b trang 112 sách giáo khoa Vật Lí 10, viên đá có khối lượng 200 g, bán kính vòng quay là 40 cm. Sợi dây hợp với phương thẳng đứng góc 56^o.

a) Tìm lực căng dây.

b) Tính độ lớn vận tốc góc của viên đá

Phương pháp giải:

Lực hướng tâm là lực cần thiết để làm cho một vật chuyển động theo đường tròn. Lực hướng tâm hướng vào quỹ đạo tròn và có độ lớn xác định bởi:

Lời giải chi tiết:

5.7

Ở một sân tập phẳng, rộng người lái xe đua phải thực hiện vòng chạy trên một dường tròn bán kính R = 121 m. Biết hệ số ma sát nghỉ cực đại giữa xe và mặt sân là .

Lấy g = 10,0 m/s². Tốc độ lớn nhất mà xe có thể chạy là bao nhiêu để không bị trượt?

Lời giải chi tiết:

Tốc độ cho phép của ô tô để nó không bị trượt trên mặt sàn phải thỏa mãn điều kiện:

Vậy tốc độ lớn nhất là 33 m/s.

5.8

Một người lái xe chữa cháy nhận lệnh đến một vụ cháy đặc biệt quan trọng. Đường nhanh nhất có thể đến đám cháy phải qua một chiếc cầu có dạng tròn với bán kính cong R = 50,0 m và cầu chỉ chịu áp lực tối đa 60 000 N. Xe chữa cháy có trọng lượng 200 000 N. Giả thiết chỉ có xe chữa cháy chuyển động tròn đều qua cầu thì cầu điều khiển xe chạy với tốc độ như thế nào để cầu không bị quá tải?

Phương pháp giải:

Một trong những giải pháp dễ thực hiện đối với người lái xe đó là tăng tốc (từ dưới chân cầu) đến vận tốc cần thiết và điều khiển xe chuyển động tròn đều qua cầu với vận tốc v.

Định luật II: Véctơ gia tốc của một vật luôn cùng hướng với lực tác dụng lên vật. Độ lớn của véctơ gia tốc tỉ lệ thuận với độ lớn của véctơ lực tác dụng lên vật và tỉ lệ nghịch với khối lượng của vật.

Lời giải chi tiết:

Khi xe chuyển động tròn đều trên cầu, theo định luật II Newton tại mọi vị trí ta luôn có:

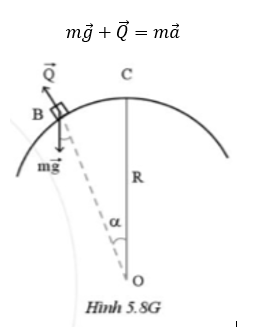
Chọn chiều dương hướng vào tâm:

Theo định luật II Newton thì áp lực xe tác dụng lên cầu có độ lớn là:

Vậy N lớn nhất khi α = 0 và giá trị đó không được vượt giới hạn áp lực cho phép của cầu.

Ta có:

Đổi: 18,7 m/s = 67,3 km/h.

5.9

Trong phòng thí nghiệm, vật nào sau đây đang bị biến dạng kéo?

A. Lò xo trong lực kế ống đang đo trọng lượng của một vật

B. Nút cao su đang nút lọ đựng dung dịch hóa chất

C. Chiếc ốc điều chỉnh ở chân để bộ thí nghiệm đo gia tốc rơi tự do

D. Bức tường

Phương pháp giải:

Trong phòng thí nghiệm, vật đang bị biến dạng kéo là Lò xo trong lực kế ống đang đo trọng lượng của một vật.

Lời giải chi tiết:

Đáp án A.

5.10

Lực đàn hồi nói chung và lực đàn hồi của lò xo nói riêng có rất nhiều ứng dụng quan trọng trong khoa học, kĩ thuật và đời sống. Trong các vật dụng sau đây, vật dụng nào không ứng dụng lực đàn hồi?

A. Bút bi                                                        B. Xe máy

C. Điều khiển từ xa dùng pin                           D. Nhiệt kế thủy ngân

Phương pháp giải:

Lực đàn hồi ở bút bi có tác dụng thu lại ngòi bút.

Lực đàn hồi ở xe máy ở nhiều bộ phận trong đó quen thuộc nhất là ở giảm xóc.

Trong điều khiển tư xa có lực đàn hồi ở bộ phận lắp pin giúp giữ viên pin cố định và tiếp xúc điện tốt.

Lời giải chi tiết:

Đáp án D.

5.11

Một lò xo nhẹ có độ cứng k = 100 N/m và chiều dài tự nhiên l_o = 10,0 cm. Người ta móc hai đầu của lò xo vào hai điểm A, B có AB = 15,0 cm. Xác định độ lớn, phương và chiều của các lực đàn hồi mà lò xo tác dụng lên điểm A và điểm B.

Lời giải chi tiết:

- Độ lớn hai lực này là:

F_A = F_B = k.(l₂ – l₁) = (100 N/m) (0,15 m – 0,10 m) = 5,00 N

- Cả hai lực cùng phương với đường nối A và B.

- Lực tác dụng vào điểm A có chiều từ A đến B, lực tác dụng vào điểm B có chiều từ B đến A.

5.12

Khi treo vào đầu dưới của một lò xo vật khối lượng m1 = 800 g thì lò xo có chiều dài 24,0 cm. Khi treo vật có khối lượng m2 = 600 g thì lò xo có chiều dài 23,0 cm. Khi treo đồng thời cả m1 và m2 thì lò xo có chiều dài bao nhiêu? Lấy g = 10,0 m/s², biết lò xo không bị quá giới hạn đàn hồi.

Phương pháp giải:

Khi treo vật khối lượng m, lúc cân bằng lực đàn hồi của lò xo có độ lớn:

F = mg

Định luật Hooke: Trong giới hạn đàn hồi, độ lớn lực đàn hồi của lò xo tỉ lệ thuận với độ biến dạng của lò xo.

F = k /ΔƖ/

Lời giải chi tiết:

Độ lớn lực đàn hồi của lò xo các lần treo lần lượt là F1 = 8,00 N và F2 = 6,00 N tương ứng với các độ dài của lò xo là:

l1 = 0,24m và l2 = 0,23m

Từ công thức Fđh = k (l – l₀)

Độ dài của lò xo khi treo cả 2 vật là:

5.13

Một diễn viên xiếc đang leo lên một sợi dây được treo thẳng đứng từ trần nhà cao. Sợ dây co giãn tuân theo định luật Hooke và có khối lượng không đáng kể. Chiều dài tự nhiên của dây là 5 m, khi diễn viên leo lên, nó dài 5,7 m. Khối lượng của diễn viên là 55 kg. Lấy g = 10,0 m/s². Tính độ cứng của sợi dây.

Phương pháp giải:

Khi treo vật khối lượng m, lúc cân bằng lực đàn hồi của lò xo có độ lớn:

F = mg

Định luật Hooke: Trong giới hạn đàn hồi, độ lớn lực đàn hồi của lò xo tỉ lệ thuận với độ biến dạng của lò xo.

F = k /ΔƖ/

Lời giải chi tiết:

P = mg = (55 kg) (10m/s²) = 550 N

=> Độ cứng của sợi dây là: k = F : ΔƖ = 790 N/m

5.14

Một lò xo có độ cứng k = 400 N/m một đầu gắn cố định. Tác dụng một lực vào đầu còn lại của lò xo và kéo đều theo phương dọc trục lò xo đến khi lò xo bị giãn 10,0 cm. Biết lò xo không bị quá giới hạn đàn hồi. Tính công của lực kéo.

Phương pháp giải:

Khi treo vật khối lượng m, lúc cân bằng lực đàn hồi của lò xo có độ lớn:

F = mg

Định luật Hooke: Trong giới hạn đàn hồi, độ lớn lực đàn hồi của lò xo tỉ lệ thuận với độ biến dạng của lò xo.

F = k /ΔƖ/

Lời giải chi tiết:

Lực kéo tăng dần từ:

F1 = 0 đến F2 = k ΔƖ₂ = (400 N/m) (0,10 m) = 40,0 N

Do lực kéo tăng đều theo quãng đường nên ta có thể tính công của nó:

Theo định luật bảo toàn và chuyển hóa năng lượng, công A chuyển hóa thành thế năng đàn hồi dự trữ trong lò xo.

5.15

Cho hệ vật như hình 5.1. Ban đầu hai vật được giữ sao cho lò xo bị nén một đoạn 10,0 cm (lò xo nhẹ và không gắn vào vật) sau đó đốt sợi dây nối hai vật. Biết độ cứng của lò xo k = 45,0 N/m; m1 = 0,50 kg; m2 = 1,50 kg. Bỏ qua lực ma sát và lực cản của không khí tác dụng lên các vật.

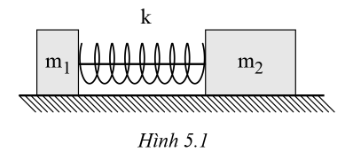
a) Tính gia tốc của mỗi vật ngay sau khi sợi dây đứt.

b) Biết rằng khi hai vật rời nhau thì m1 chuyển động với tốc độ là 3,00 m/s. Tính tốc độ của m2.

Lời giải chi tiết:

a) Ngay sau khi dây nối đứt, theo phương ngang m1 và m2 chỉ chịu tác dụng của lực đàn hồi lò xo:

F1 = F2 = k ΔƖ = (45N/m) (0,10m) = 4,50 N

Gia tốc của m1:

b) Chọn chiều dương hướng sang trái và mốc là một điểm gắn với mặt bàn.

Theo định luật bảo toàn động lượng:

5.16

Cho các dụng cụ sau:

- Giá thí nghiệm đã gắn thước đo dộ dài: 1 cái.

- Lò xo chưa biết độ cứng: 1 cái.

- Vật có móc treo đã biết trọng lượng là Po: 1 quả

- Một vật X có móc treo cần xác định trọng lượng Px.

Hãy trình bày một phương án thí nghiệm để tìm trọng lượng của vật X.

Lời giải chi tiết:

- Bước 1: Treo lò xo lên giá thí nghiệm, xác định chiều dài ban đầu của lò xo l₁.

- Bước 2: Treo vật trọng lượng P_o vào đầu dưới của lò xo rồi xác định chiều dài l₂ của lò xo.

- Bước 3: Thay vật có trọng lượng P_o bằng vật cần xác định trọng lượng P_x và xác định chiều dài của lò xo l₃.

Ta có:

5.17

Cho các dụng cụ sau:

- Lực kế: 1 cái

- Thước đo độ dài: 1 cái

- Lò xo cần xác định độ cứng: 1 cái

Hãy trình bày một phương án thí nghiệm để đo độ cứng của lò xo đã cho.

Lời giải chi tiết:

Bước 1: Đo chiều dài tự nhiên của lò xo, móc 1 đầu lò xo vào lực kế sau đó chỉnh số 0 cho lực kế (cần chú ý nếu dùng lực kế lò xo ống cần treo lực kế thẳng đứng).

Bước 2: Kéo đầu còn lại của lò xo theo phương thẳng đúng và giữ cố định vị trí. Đo độ dài của lò xo, và đọc số chỉ lực kế ta tính được độ dãn.

Bước 3: Thực hiện lại bước 2 từ 3 đến 5 lần với các số liệu về độ dãn của lò xo khác nhau và xử lí số liệu.

5.18

Một nhóm học sinh tìm hiểu độ cứng của lò xo. Họ dùng các lò xo giống nhau có cùng chiều dài và cùng độ cứng kết hợp thành hệ hai lò xo mắc nối tiếp và hệ hai lò xo mắc song song. Sau đó, họ treo các vật với trọng lượng khác nhau vào đầu dưới mỗi hệ lò xo treo thẳng đứng, rồi đo độ giãn. Kết quả đo được cho ở bảng dưới đây:

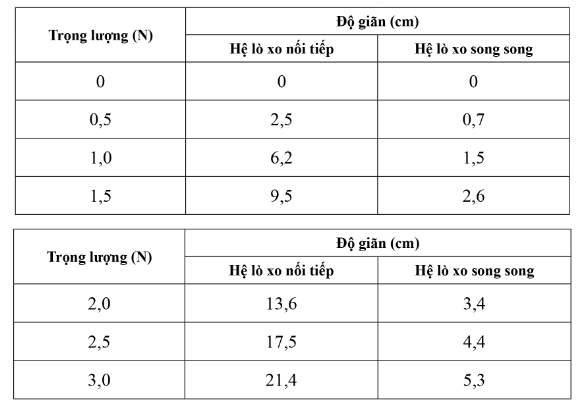
a) Với mỗi hệ lò xo nối tiếp và hệ lò xo song song, vẽ đồ thị biểu diễn liên hệ giữa lực tác dụng vào đầu dưới hệ lò xo và độ giãn của hệ.

b) Sử dụng đồ thị để tính độ cứng cho mỗi hệ lò xo

c) Sử dụng đồ thị để chứng tỏ rằng độ cứng của hệ hai lò xo nối tiếp nhau bằng một phần tư độ cứng của hệ hai lò xo song song.

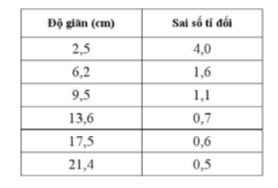
d) Đối với hệ hai lò xo nối tiếp, tính sai số tỉ đối trong mỗi lần đo độ giãn, nếu sai số tuyệt đối là ± 0,1 cm.

Phương pháp giải:

Định luật Hooke: Trong giới hạn đàn hồi, độ lớn lực đàn hồi của lò xo tỉ lệ thuận với độ biến dạng của lò xo.

F = k /ΔƖ/

Lời giải chi tiết:

a)

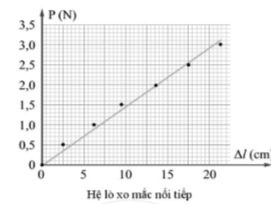
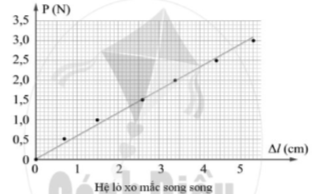
b) Độ cứng của hệ hai lò xo nối tiếp là 0,14 N/cm, của hệ hai lò xo song song là 0,58 N/cm.

c) Tỉ số độ cứng là: 0,58 : 0,14 = 4

d) Kết quả tính sai số: