Phần câu hỏi bài 9 trang 135 Vở bài tập toán 8 tập 2

Câu 16

Hình chóp tứ giác đều có cạnh đáy \(a = 15cm\) và chiều cao hình chóp là \(h = 12,5cm\).

Thể tích của hình chóp là:

A. \(937,5c{m^3}\)                     B. \(1050c{m^3}\)

C. \(781,25c{m^3}\)                   D. \(250c{m^3}\)

Khoanh tròn vào chữ cái trước khẳng định đúng.

Phương pháp giải:

Sử dụng công thức tính thể tích hính chóp \(V = \dfrac{1}{3}Sh\) với \(S\) là diện tích đáy, \(h\) là chiều cao hình chóp

Lời giải chi tiết:

Diện tích đáy hình chóp là: \(15.15 = 225\left( {c{m^2}} \right)\).

Thể tích của hình chóp là: \(\dfrac{1}{3}.225.12,5 = 937,5\left( {c{m^3}} \right)\).

Chọn A. 

Câu 17

Hình chóp tứ giác đều có thể tích bằng \(34,5c{m^3}\) và có chiều cao là \(4,5cm\). Cạnh đáy của hình chóp (lấy đến hai chữ số thập phân) là:

A. \(4,79cm\)                     B. \(4,80cm\)

C. \(5,39cm\)                     D. \(2,77cm\)

Khoanh tròn vào chữ cái trước khẳng định đúng.

Phương pháp giải:

- Tính diện tích đáy \(S = \dfrac{{3V}}{h}\) với \(V\) là thể tích hình chóp, \(h\) là chiều cao hình chóp

- Tính cạnh và kết luận. 

Lời giải chi tiết:

Diện tích đáy hình chóp là \(\dfrac{{3.34,5}}{{4,5}} = 23\left( {c{m^2}} \right)\).

Cạnh đáy là \(\sqrt {23}  \approx 4,80\left( {cm} \right)\). 

Chọn B.

Câu 18

Hình chóp tam giác đều \(S.ABC\) có thể tích bằng \(123,5c{m^3}\) và có cạnh đáy \(a = 10cm\).

Chiều cao của hình chóp (lấy đến hai chữ số thập phân) là:

A. \(9,18cm\)                      B. \(9,17cm\)

C. \(8,56cm\)                      D. \(8,55cm\)

Khoanh tròn vào chữ cái trước khẳng định đúng.

Phương pháp giải:

Sử dụng công thức tính chiều cao hình chóp \(h = \dfrac{{3V}}{S}\) với \(S\) là diện tích đáy, \(V\) là thể tích hình chóp 

Lời giải chi tiết:

Gọi đáy hình chóp là tam giác đều \(ABC\) có cạnh bằng \(10cm\).

Gọi \(H\) là trung điểm của \(BC\) thì \(AH\) vừa là đường trung tuyến vừa là đường cao của tam giác. 

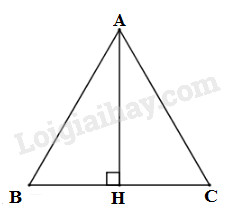
Tam giác \(ABH\) vuông tại \(H\) có \(AB = 10cm,BH = 5cm\). 

Ta có: \(AH = \sqrt {A{B^2} - B{H^2}} \) \( = \sqrt {{{10}^2} - {5^2}}  \approx 8,66\left( {cm} \right)\)

Diện tích tam giác \(ABC\) là: \(S = \dfrac{1}{2}BC.AH\)\( = \dfrac{1}{2}.10.8,66 = 43,30\left( {c{m^2}} \right)\)

Chiều cao hình chóp là: \(3.123,5:43,30 \approx 8,56\left( {cm} \right)\).

Chọn C.