Phần câu hỏi bài 5 trang 155, 156 Vở bài tập toán 8 tập 1

Câu 13.

Một hình chữ nhật có các cạnh kề bằng \(6m\) và \(8m\). Diện tích tứ giác có bốn đỉnh là trung điểm bốn cạnh của hình chữ nhật bằng

\(\begin{gathered}
(A)\,\,48{m^2} \hfill \\
(B)\,\,28{m^2} \hfill \\
(C)\,24{m^2} \hfill \\
(D)\,12{m^2} \hfill \\
\end{gathered} \)

Phương pháp giải:

- Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa độ dài cạnh ấy.

- Diện tích hình chữ nhật có kích thước hai cạnh \(a,b\) là \(S=a.b\).

- Diện tích hình thoi bằng nửa tích độ dài hai đường chéo. 

\(S=\dfrac{1}{2}{d_1}.{d_2}\)

Lời giải:

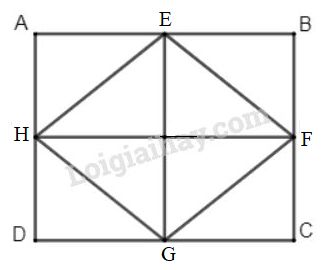
Xét hình chữ nhật \(ABCD\) có \(E, F, G, H\) theo thứ tự là trung điểm của \(AB, BC, CD, DA\).

Ta có \(\Delta AEH = \Delta BEF = \Delta CGF \)\(\,= \Delta DGH\,\,\left( {c.g.c} \right)\)

suy ra \(EH=EF=GF=GH\) nên tứ giác \(EFGH\) là hình thoi.

Ta thấy tám tam giác vuông trong hình bằng nhau nên có diện tích bằng nhau. Hình thoi gồm \(4\) tam giác vuông, hình chữ nhật \(ABCD\) gồm \(8\) tam giác vuông nên diện tích hình thoi bằng \(\dfrac{1}{2}\) diện tích hình chữ nhật.

\({S_{ABCD}} = AD.DC \)

nên \({S_{EFGH}} = \dfrac{1}{2}AD.DC=\dfrac{1}{2}.6.8 \)\(\,= 24\,\,\left( {{m^2}} \right)\)

Chọn C.

Câu 14.

Một hình thoi có cạnh \(a\), một góc bằng \(60^{\circ}\). Diện tích hình thoi đó bằng

\(\begin{gathered}
(A)\,{a^2}\sqrt 3 \,\, \hfill \\
(B)\,\frac{{{a^2}\sqrt 3 }}{2} \hfill \\
(C)\,\,\frac{{{a^2}\sqrt 3 }}{4} \hfill \\
(D)\,\frac{{{a^2}}}{2} \;\;\;\;\hfill \\
\end{gathered} \)

Phương pháp giải:

Sử dụng: 

- Tam giác đều là tam giác có ba cạnh bằng nhau.

- Định lí Pytago: Bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.

- Diện tích hình bình hành bằng tích của một cạnh với chiều cao ứng với cạnh đó.

\(S = ah\)

- Diện tích hình thoi bằng nửa tích độ dài hai đường chéo.

\(S=\dfrac{1}{2}{d_1}.{d_2}\)

Lời giải:

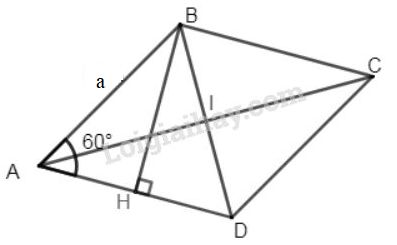
Xét hình thoi \(ABCD\) có \(AB = a\), \(\widehat{A}\) = \(60^{\circ}\)

\(∆ABD\) là tam giác đều vì \(AB=AD\) và  \(\widehat{A}\) = \(60^{\circ}\).

Kẻ \(BH\bot AD\), ta có \(AH=HD=\dfrac{a}{2}\) (vì \(BH\) là đường cao đồng thời là trung tuyến trong tam giác đều)

Áp dụng định lí Pytago vào tam giác vuông \(ABH\), ta có

\(B{H^2} = A{B^2} - A{H^2}={a^2} - {\left( {\dfrac{a}{2}} \right)^2} \)\(\,= {a^2} - \dfrac{{{a^2}}}{4} = \dfrac{{3{a^2}}}{4}\) nên \( BH =\dfrac{{a\sqrt 3 }}{2}\)

\({S_{ABCD}}= AD.BH = a.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{{a^2}\sqrt 3 }}{2}\)

Chọn B.

Câu 15.

Hình thang cân \(ABCD(AB//CD)\) có \(AC\bot BD, AC=10\,cm\). Diện tích hình thang đó bằng

\(\eqalign{
& (A)\,\,40c{m^2} \cr
& (B)\,100c{m^2} \cr
& (C)\,200c{m^2} \cr
& (D)\,50c{m^2} \cr} \)

Phương pháp giải:

Sử dụng: 

- Diện tích của một tứ giác có hai đường chéo vuông góc bằng nửa tích độ dài hai đường chéo đó.

\({S_{ABCD}}=\dfrac{1}{2} AC. BD\)

- Hình thang cân có hai đường chéo bằng nhau.

Lời giải:

\(ABCD\) là hình thang cân nên \(AC=BD=10cm\)

\(AC\bot BD\) do đó diện tích hình thang \(ABCD\) là

\({S_{ABCD}} = \dfrac{1}{2}AC.BD = \dfrac{1}{2}.10.10 \)\(\,= 50\,\left( {c{m^2}} \right)\)

Chọn D.