Phần câu hỏi bài 5 trang 122 Vở bài tập toán 9 tập 1

Câu 9

Hãy khoanh tròn vào chữ cái đứng trước đáp án đúng

Cho tam giác ABC với các đường trung tuyến AD, BE, CF. Gọi G là trọng tâm của tam giác ABC. Ta có:

(A) BC là tiếp tuyến của đường tròn (G ; GD)

(B) AC là tiếp tuyến của đường tròn (G ; GE)

(C) AB là tiếp tuyến của đường tròn (G ; GF)

(D) Ba khẳng định trên đều sai.

Phương pháp giải:

Vận dụng kiến thức : Nếu đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng là một tiếp tuyến của đường tròn.

Lời giải chi tiết:

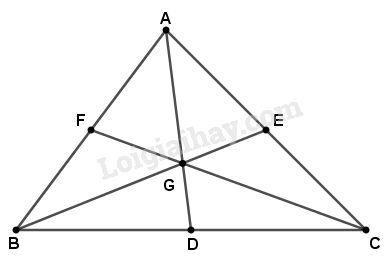
Đường tròn \(\left( {G;GD} \right)\)  có bán kính \(GD\) không vuông góc với \(BC\) nên nhận xét (A) sai.

Tương tự như vậy, kiểm tra các nhận xét (B) và (C).

Chọn D.

Câu 10

Cho tam giác ABC với các đường phân giác AD, BE và CF. Gọi O là giao điểm của ba đường phân giác đó; gọi H là chân đường vuông góc kẻ từ O đến BC. Ta có:

(A) Cả AB, AC, AD đều là tiếp tuyến của đường tròn (O ; OH)

(B) AB là tiếp tuyến của đường tròn (O ; OF)

(C) AC là tiếp tuyến của đường tròn (O ; OE)

(D) BC là tiếp tuyến của đường tròn (O ; OD).

Phương pháp giải:

- Vẽ hình theo các giả thiết đã cho.

- Kiểm tra các nhận xét đã cho bằng cách vận dụng kiến thức : Nếu khoảng cách từ tâm của đường tròn đến một đường thẳng bằng bán kính của đường tròn thì đường thẳng đó là tiếp tuyến của đường  tròn.

Lời giải chi tiết:

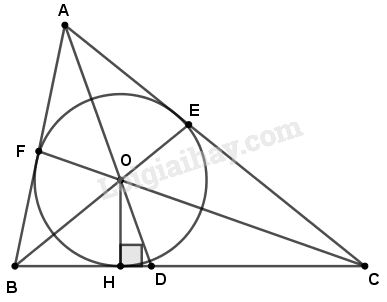
Ta có \(O\) là giao điểm của ba đường phân giác trong tam giác \(ABC\) nên \(O\) là tâm đường tròn nội tiếp tam giác đó.

\(OH\) là khoảng cách từ tâm \(O\) đến \(BC.\)

Vậy \((O;OH)\) tiếp xúc với các cạnh \(AB,BC,CA\) hay  AB, AC, AD đều là tiếp tuyến của đường tròn (O ; OH).

Chọn A.