Giải mục 2 trang 61, 62 SGK Toán 8 - Cùng khám phá

Hoạt động 3

1. Vẽ hai tứ giác bất kì. Đo và tính tổng các góc của mỗi tứ giác. Em có nhận xét gì về hai tổng này?
2. So sánh tổng các góc của tứ giác \(ABCD\) với tổng các góc của hai tam giác \(ABD\) và \(BCD\), từ đó tính tổng các góc của tứ giác \(ABCD\)

Phương pháp giải:

Vẽ hai tứ giác bất kì sau đó đo và tính tổng các góc của mỗi tứ giác. Nhận xét về hai tổng.

So sánh tổng các góc của tứ giác \(ABCD\) với tổng các góc của hai tam giác \(ABD\) và \(BCD\), từ đó tính tổng các góc của tứ giác \(ABCD\)

Lời giải chi tiết:

a)      

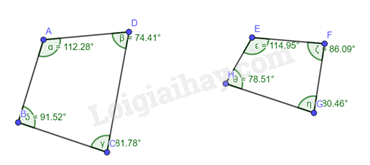
Nhận xét: Tổng của cả hai tứ giác đều bằng \(360^\circ \).

b)    Ta có:

Tổng các góc của tam giác \(ABD\) là \(112,28 + 34 + 33,72 = 180^\circ \)

Tổng các góc của tam giác \(BCD\) là: \(40,41 + 81,78 + 57,8 = 180^\circ \)

Vậy tổng của tứ giác \(ABCD\) là \(180^\circ  + 180^\circ  = 360^\circ \).

Luyện tập 3

Tính số đo góc D và góc E của các tứ giác trong Hình 3.20.

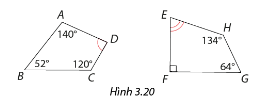
Phương pháp giải:

Tổng các góc của một tứ giác bằng \(360^\circ \). Từ đó tìm được góc D và E.

Lời giải chi tiết:

Ta có số đo góc D là: \(\widehat D = 360^\circ  - \left( {\widehat A + \widehat B + \widehat C} \right) = 360^\circ  - \left( {140^\circ  + 52^\circ  + 120^\circ } \right) = 48^\circ \)

Số đo góc E là: \(\widehat E = 360^\circ  - \left( {\widehat H + \widehat G + \widehat F} \right) = 360^\circ  - \left( {134^\circ  + 64^\circ  + 90^\circ } \right) = 72^\circ \).

Vận dụng

Cánh diều hình tứ giác \(ABCD\) có \(\widehat D = 107^\circ ,\widehat B = 63^\circ \) và \(\widehat A = \widehat C\) (Hình 3.21). Tính số đo góc A và góc C của cánh diều.

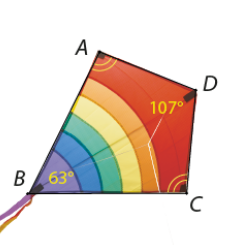
Phương pháp giải:

Tổng các góc của một tứ giác bằng \(360^\circ \). Từ đó tìm được góc A và C.

Lời giải chi tiết:

Gọi số đo góc \(\widehat A\) là \(x\) thì \(\widehat A = \widehat C = x\)

Ta có:

 \(\begin{array}{l}360^\circ  = \widehat A + \widehat B + \widehat C + \widehat D = x + x + 107 + 63 = 2x + 170\\ =  > x = \left( {360^\circ  - 170^\circ } \right):2 = 190^\circ :2 = 95^\circ \end{array}\)

Vậy \(\widehat A = \widehat C = 95^\circ \).