Giải mục 2 trang 114, 115, 116 SGK Toán 8 tập 2 - Kết nối tri thức

Hoạt động 1

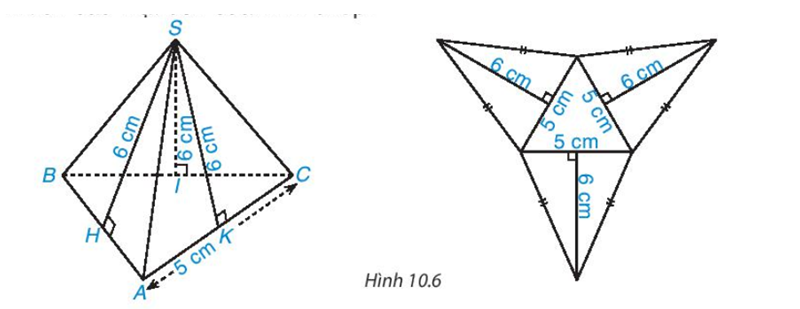
Quan sát hình chóp tam giác đều và hình khai triển của nó. Hãy tính tổng diện tích các mặt bên của hình chóp.

Phương pháp giải:

- Nhận thấy các mặt bên của hình chóp được tạo bởi 3 hình tam giác

- Tín diện tích một tam giác.

Lời giải chi tiết:

Nhận thấy các mặt bên của hình chóp được tạo bởi 3 hình tam giác

Diện tích của một tam giác là: \(\frac{1}{2}\)⋅6⋅5=15(cm²)

=> Tổng diện tích các mặt bên là: 15.3=45(cm²)

Hoạt động 2

Hãy tính tích của nửa chu vi mặt đáy với trung đoạn của hình chóp tam giác đều. So sánh kết quả vừa tính với tổng diện tích các mặt bên của hình chóp 

Phương pháp giải:

Tính các kết quả theo yêu cầu bài toán và so sánh

Lời giải chi tiết:

Có nửa chu vi đáy là: \(\frac{1}{2}.\)(5+5+5) = \(\frac{{15}}{2}\)(cm)

Có trung đoạn là: 6cm

=> Tích của nửa chu vi mặt đáy với trung đoạn của hình chóp tam giác đều là: \(\frac{{15}}{2}.6 = 45\)

=> Kết quả bằng với tổng diện tích các mặt bên của hình chóp

Luyện tập

Tính diện tích xung quanh của hình chóp tam giác đều S.MNP trong Hình 10.8, biết IP = 3 cm và cạnh bên SP = 5 cm

Phương pháp giải:

Tính nửa chu vi đáy của tam giác MNP

Tính diện tích xung quanh của hình chóp tam giác đều S.MNP

Lời giải chi tiết:

Xét tam giác SIP vuông tại I, có

\(\begin{array}{l}S{I^2} = S{P^2} - I{P^2}\\S{I^2} = {5^2} - {3^2}\\ \Rightarrow SI = 4cm\end{array}\)

- Vì tam giác SMP cân tại S => đường cao SI đồng thời là đường trung tuyến của tam giác SMP => IM=IP=3cm => MP = 6 cm

Xét tam giác đều MNP có \(p = \frac{1}{2}\left( {6 + 6 + 6} \right) = 9(cm)\)

Diện tích xung quanh của hình chóp tam giác đều S. MNP:

\({S_{xp}} = 9.4 = 36\left( {c{m^2}} \right)\)

Vận dụng

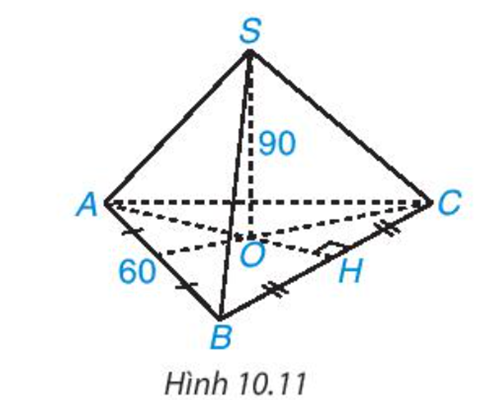
Đỉnh Fansipan (Lào Cai) cao 3 143m, là đỉnh núi cao nhất Đông Dương. Trên đỉnh núi. người ta đặt một chóp làm bằng inox có dạng hình chóp tam giác đều cạnh đáy 60 cm, chiều cao 90 m. Hỏi tổng diện tích các mặt bên của hình chóp là bao nhiêu.

Phương pháp giải:

Tính diện tích xung quanh của hình chóp tam giác đều S.ABC

Lời giải chi tiết:

Nửa chu vi của hình tam giác đều ABC là:

\(p = \frac{1}{2}\left( {60 + 60 + 60} \right) = 90(cm)\)

Diện tích xung quanh của hình chóp tam giác đều S. ABC là:

\({S_{xq}} = 90.90 = 8100(c{m^2})\)

Vậy diện tích các mặt bên của hình chóp tam giác đều là 8100 cm²