Giải mục 1 trang 74, 75 SGK Toán 8 – Cánh diều
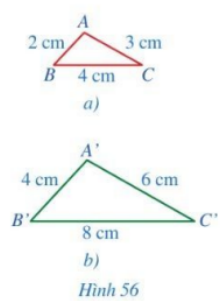
Quan sát Hình 56 và so sánh các tỉ số:
Hoạt động 1
Quan sát Hình 56 và so sánh các tỉ số: \(\frac{{A'B'}}{{AB}};\,\,\frac{{A'C'}}{{AC}};\,\,\frac{{B'C'}}{{BC}}\).
Phương pháp giải:
Tính tỉ số giữa các cạnh rồi so sánh.
Lời giải chi tiết:
\(\begin{array}{l}\frac{{A'B'}}{{AB}} = \frac{2}{4} = \frac{1}{2}\\\frac{{A'C'}}{{AC}} = \frac{3}{6} = \frac{1}{2}\\\frac{{B'C'}}{{BC}} = \frac{4}{8} = \frac{1}{2}\end{array}\)
Ta thấy \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}}\)
Luyện tập 1
Cho tam giác ABC có trọng tâm G. Gọi A’, B’, C’ lần lượt là trung điểm của AG, BG, CG. Chứng minh \(\Delta A'B'C' \backsim\Delta ABC\).
Phương pháp giải:
Tính tỉ số giữa các cạnh rồi chứng minh đồng dạng bằng trường hợp đồng dạng thứ nhất.
Lời giải chi tiết:
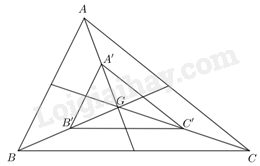
Vì A’, B’, C’ lần lượt là trung điểm của AG, BG, CG nên A’B’, B’C’, A’C’ lần lượt là đường trung bình của các tam giác AGB, BGC, AGC.
Khi đó: \(\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = \frac{{A'C'}}{{AC}} = \frac{1}{2}\)
Xét tam giác A’B’C’ và tam giác ABC có:
\(\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = \frac{{A'C'}}{{AC}} = \frac{1}{2}\)
Vậy \(\Delta A'B'C' \backsim\Delta ABC\) (c-c-c)
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải mục 1 trang 74, 75 SGK Toán 8 – Cánh diều timdapan.com"







