Bài 14. Khối lượng riêng trang 73, 74, 75, 76 Khoa học tự nhiên 8 - Cánh diều

KĐ

Trong một số trường hợp, có thể tính được khối lượng của một vật qua kích thước của nó mà không cần dùng cân. Ví dụ, có thể tính được khối lượng của nước trong bể bơi khi biết kích thước của bể. Dựa trên cơ sở nào mà có thể làm được điều đó?

Phương pháp giải:

Dựa vào kinh nghiệm và tìm kiếm thông tin trên internet để đưa ra dự đoán.

Lời giải chi tiết:

Bình thường khi nhắc đến nước chúng ta hay nói đến một lít nước bằng một kg nước, vậy nên khi biết thể tích nước trong bể bơi có thể tính được khối lượng của nước.

Giữa khối lượng và thể tích có một mối liên hệ nên từ thể tích có thể tính được khối lượng của vât.

CH 1

So sánh khối lượng nước chứa trong một bình 20L và trong một chai 0.5L

Phương pháp giải:

Dựa vào công thức \(D = \frac{m}{V}\)để so sánh khối lượng của nước trong bình và chai.

Lời giải chi tiết:

Ta có: m₁ là khối lượng nước trong bình, m₂ là khối lượng nước trong chai, V₁ là thể tích nước trong bình, V₂ là thể tích nước trong chai

Do \(D = \frac{m}{V}\)nên \(\frac{{{m_1}}}{{{V_1}}} = \frac{{{m_2}}}{{{V_2}}}\)(do cùng là nước)

⇨    \(\frac{{{m_1}}}{{20}} = \frac{{{m_2}}}{{0.5}} \Rightarrow \frac{{{m_1}}}{{{m_2}}} = \frac{{20}}{{0.5}} = 40 \Rightarrow {m_1} = 40{m_2}\)

Vậy khối lượng nước trong bình gấp 40 lần khối lượng nước trong chai.

CH 2

Nêu một số đơn vị đo khối lượng riêng.

Phương pháp giải:

Căn cứ vào định nghĩa khối lượng riêng để nêu đơn vị đo.

Lời giải chi tiết:

Một số đơn vị đo khối lượng riêng: kg/m³; g/m³; g/cm³; g/mL; kg/L

CH 1

Một bể bơi có chiều dài 20m, chiều rộng 8m, độ sâu của nước là 1,5m, tính khối lượng của nước trong bể.

Phương pháp giải:

Dựa vào công thức \(D = \frac{m}{V}\)để tính khối lượng của nước.

Lời giải chi tiết:

Khối lượng riêng của nước D = 1000 kg/m³

Thể  tích của phần nước trong bể bơi là:
V = 20 x 8 x 1,5 = 240 (m³)

Khối lượng nước trong bể bơi là:

m = D.V = 1000.240 = 240.000 (kg)

CH 2

Thảo luận, đề xuất các cách xác định khối lượng riêng của một lượng chất lỏng.

Phương pháp giải:

Dựa vào các kiến thức đã học về khối lượng riêng để xác định, chú ý đến cân nặng của các dụng cụ dùng để đo.

Lời giải chi tiết:

Đề xuất phương án: để xác định được khối lượng riêng cần xác định khối lượng và thể tích của lượng chất lỏng đang xét đến.

- Xác định khối lượng của lượng chất lỏng bằng cân, chú ý trừ đi khối lượng của cốc đong dùng để đựng nước.

- Xác định thể tích của lượng nước thông qua vạch chia trên cốc đong.

- Khối lượng riêng của chất lỏng được xác định theo công thức \(D = \frac{m}{V}\)

CH 3

Khi đổ chất lỏng vào cốc đong cần chú ý điều gì?

Phương pháp giải:

Dựa vào kinh nghiệm của bản thân và tìm hiểu các thông tin trên internet.

Lời giải chi tiết:

Chú ý:

- Đặt cốc đong đứng thẳng.

- Đổ chất lỏng từ từ, tránh làm đổ chất lỏng ra phía ngoài.

- Lựa chọn lượng chất lỏng phù hợp với GHĐ của cốc đong.

CH 1

Tính khối lượng của một khối nhôm hình hộp chữ nhật, có chiều dài 10 cm, chiều rộng 3 cm, chiều cao 5 cm.

Phương pháp giải:

Dùng công thức \(D = \frac{m}{V}\)để tính khối lượng của khối nhôm.

Lời giải chi tiết:

Khối lượng riêng của nhôm D = 2700 kg/m³

Thể tích khối nhôm là:

V = 10 x 3 x 5 = 150 cm³ = 1,5x10^-4 m³

- Khối lượng của khối nhôm là:

\(D = \frac{m}{V} \Rightarrow m = D.V = 2700.1,{5.10^{ - 4}} = 0.405\)kg

CH 2

Thảo luận, đề xuất cách xác định khối lượng riêng của một vật có hình dạng bất kỳ.

Phương pháp giải:

Dựa vào các kiến thức đã học về khối lượng riêng để xác định.

Lời giải chi tiết:

Đề xuất phương án: để xác định được khối lượng riêng cần xác định khối lượng và thể tích của vật đang xét đến.

- Xác định khối lượng của vật đó bằng cân.

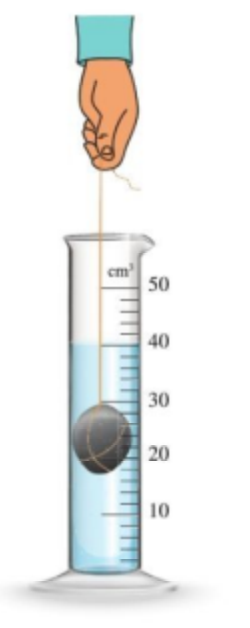
- Xác định thể tích của vật thông qua phương pháp xác định thể tích vật rắn không thấm nước:

+ Đổ nước vào ống đong, thả vật vào trong ống đong, thể tích của vật bằng thể tích nước dâng lên thêm.

+ Hoặc vật không vừa ống đong thì sử dụng bình tràn, thể tích vật là phần nước tràn từ bình tràn sang ống đong.

- Khối lượng riêng của chất lỏng được xác định theo công thức \(D = \frac{m}{V}\)

CH 1

Một nhóm học sinh tiến hành xác định khối lượng riêng của các viên bi giống nhau. Một bạn tiến hành thí nghiệm với một viên bi. Một bạn khác đề nghị đo tổng khối lượng và thể tích của 10 viên bi. Cách làm nào cho kết quả chính xác hơn? Vì sao?

Phương pháp giải:

Dựa vào kinh nghiệm của bản thân và tìm hiểu các thông tin trên internet.

Lời giải chi tiết:

Cách làm của bạn thứ hai khi đo tổng khối lượng và thể tích của 10 viên bi sẽ chính xác hơn. Vì một viên bi có khối lượng và thể tích nhỏ nên nếu chỉ đo 1 viên có thể vạch chia nhỏ nhất của dụng cụ đo sẽ không đọc được hết, dẫn đến kết quả sẽ bị làm tròn lên nhiều.

CH 2

1. Đề xuất các phương án xác định khối lượng riêng của một chiếc chìa khóa.

2. Ước tính tổng khối lượng không khí ở trong lớp học của em khi đóng kín cửa.

3. Tại sao cùng một nơi trên mặt đất, trọng lượng của vật tỉ lệ với khối lượng của nó. Chứng minh rằng: Trọng lượng riêng của vật (kí hiệu là d): d = 10D

Phương pháp giải:

Dựa vào kinh nghiệm của bản thân và tìm hiểu các thông tin trên internet.

Lời giải chi tiết:

1. Đề xuất phương án: để xác định được khối lượng riêng cần xác định khối lượng và thể tích của chiếc chìa khóa.

- Xác định khối lượng của chìa khóa bằng cân.

- Xác định thể tích của chìa khóa thông qua phương pháp xác định thể tích vật rắn không thấm nước:

Đổ nước vào ống đong, thả chìa khóa vào trong ống đong, thể tích của chìa khóa bằng thể tích nước dâng lên thêm.

- Khối lượng riêng của chất lỏng được xác định theo công thức \(D = \frac{m}{V}\)

2. Không khí có khối lượng riêng D = 1,29 kg/m³

Phòng học của em có kích thước khoảng 3 x 2 x 5 (m) (thể tích tùy từng hs ước lượng khác nhau)

=> Thể tích của phòng học khoảng: V = 3 x 2 x 5 = 30 m³

=> Tổng khối lượng không khí trong phòng khoảng: m = D.V = 1,29 x 30 = 38,7 kg (thể tích ước lượng khác nhau nên khối lượng thu được cũng sẽ khác nhau)

3.

- Trọng lượng của vật là độ lớn lực hút của Trái Đất tác dụng lên vật, được tính theo công thức P = 10m trong đó P là trọng lượng, m là khối lượng nên trọng lượng sẽ tỉ lệ thuận với khối lượng tại cùng một nơi đang xét.

- Trọng lượng riêng của vật được tính bằng \(d = \frac{P}{V}\)

\( \Rightarrow d = \frac{{10m}}{V} = 10D\)

CH 3

Có nhiều trường hợp không thể dùng cân để xác định khối lượng của vật. Khi đó, nếu biết khối lượng riêng của chất tạo nên vật, ta có thể xác định được khối lượng của vật. Ví dụ, các kim tự tháp Ai Cập được dựng lên bằng những khối đá hoa cương hình lập phương. Nếu biết khối lượng của mỗi khối đá hình lập phương với cạnh 10 cm là 2,75kg, người ta tính được khối lượng của các khối đá dùng để dựng lên kim tự tháp. Người ta đã làm điều đó như thế nào?

Phương pháp giải:

Dựa vào kinh nghiệm của bản thân và tìm hiểu các thông tin trên internet.

Lời giải chi tiết:

Thể tích của khối đá hoa cương có cạnh là 10 cm là:

V = 10 x 10 x 10 = 1000 cm³

Khối lượng riêng của đá hoa cương dựng lên kim tự tháp là: \(d = \frac{m}{V} = \frac{{2,75}}{{0,001}} = 2750\)kg/m³

Vậy khi biết được khối lượng riêng của đá hoa cương rồi, chỉ cần biết thêm thể tích của viên đá hoa cương dùng để dựng lên kim tự tháp sẽ xác định được khối lượng đá đá dùng để dựng kim tự tháp.