B. Hoạt động thực hành - Bài 70 : So sánh hai phân số cùng mẫu số
Giải Bài 70 : So sánh hai phân số cùng mẫu số phần hoạt động thực hành trang 33, 34 sách VNEN toán lớp 4 với lời giải dễ hiểu
Câu 1
So sánh hai phân số:
a) \(\dfrac{5}{9}\) và \(\dfrac{7}{9}\) b) \(\dfrac{7}{6}\) và \(\dfrac{6}{6}\)
c) \(\dfrac{3}{{14}}\) và \(\dfrac{6}{{14}}\) d) \(\dfrac{8}{8}\) và \(\dfrac{2}{8}\)
Phương pháp giải:
Trong hai phân số có cùng mẫu số :
• Phân số nào có tử số bé hơn thì bé hơn.
• Phân số nào có tử số lớn hơn thì lớn hơn.
• Nếu tử số bằng nhau thì hai phân số đó bằng nhau.
Lời giải chi tiết:
a) \(\dfrac{5}{9} < \dfrac{7}{9}\) (vì \(5 < 7\)) b) \(\dfrac{7}{6} > \dfrac{6}{6}\) (vì \(7>6\))
c) \(\dfrac{3}{{14}} < \dfrac{6}{{14}}\) (vì \(3<6\)) d) \(\dfrac{8}{8} > \dfrac{2}{8}\) (vì \(8>2\))
Câu 2
a) Đọc kĩ nhận xét sau và nói với bạn cách so sánh với 1.
• \(\dfrac{3}{4} < \dfrac{4}{4}\) mà \(\dfrac{4}{4} = 1\) nên \(\dfrac{3}{4} < 1.\)
Nếu tử số bé hơn mẫu số thì phân số bé hơn 1.
• \(\dfrac{7}{4} > \dfrac{4}{4}\) mà \(\dfrac{4}{4} = 1\) nên \(\dfrac{7}{4} < 1.\)
Nếu tử số lớn hơn mẫu số thì phân số lớn hơn 1.
b) So sánh các phân số sau với 1: \(\dfrac{5}{6}\,\,;\,\,\,\,\dfrac{3}{2}\,;\,\,\,\,\dfrac{9}{{19}}\,;\,\,\,\,\dfrac{7}{7}\,;\,\,\,\,\dfrac{{49}}{{46}}\,;\,\,\,\,\dfrac{{32}}{{71}}.\)
Phương pháp giải:
- Nếu tử số bé hơn mẫu số thì phân số bé hơn 1.
- Nếu tử số lớn hơn mẫu số thì phân số lớn hơn 1.
- Nếu tử số bằng mẫu số thì phân số bằng 1.
Lời giải chi tiết:
a) Cách so sánh phân số với 1:
- Nếu tử số bé hơn mẫu số thì phân số đó bé hơn 1.
- Nếu tử số lớn hơn mẫu số thì phân số đó lớn hơn 1.
- Nếu tử số bằng mẫu số thì phân số bằng 1.
b) So sánh các phân số với 1:
• \(\dfrac{5}{6} < 1\) (vì 5 < 6) • \(\dfrac{3}{2} > 1\) (vì 3 > 2)
• \(\dfrac{9}{{19}} < 1\) ( vì 9 < 19) • \(\dfrac{7}{7} = 1\) ( vì 7 = 7)
• \(\dfrac{{49}}{{46}} > 1\) (vì 49 > 46) • \(\dfrac{{32}}{{71}} < 1\) ( vì 32 < 71)
Câu 3
Nối (theo mẫu):
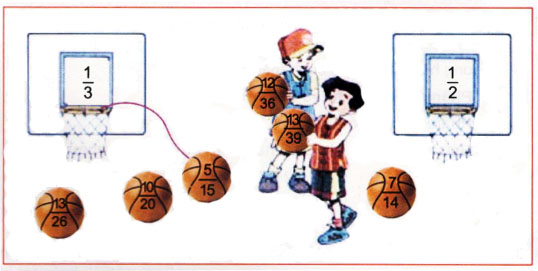
Phương pháp giải:
Rút gọn các phân số đã cho thành phân số tối giản, từ đó tìm các phân số bằng với phân số \(\dfrac{1}{3}\) hoặc \(\dfrac{1}{2}\).
Lời giải chi tiết:
Ta có :
\(\dfrac{{13}}{{26}} = \dfrac{{13:13}}{{26:13}} = \dfrac{1}{2}\,\,;\) \(\dfrac{{10}}{{20}} = \dfrac{{10:10}}{{20:10}} = \dfrac{1}{2}\,\,;\)
\(\dfrac{5}{{15}} = \dfrac{{5:5}}{{15:5}} = \dfrac{1}{3}\,\,;\) \(\dfrac{{12}}{{36}} = \dfrac{{12:12}}{{36:12}} = \dfrac{1}{3}\,\,;\)
\(\dfrac{{13}}{{39}} = \dfrac{{13:13}}{{39:13}} = \dfrac{1}{3}\,\,;\) \(\dfrac{7}{{14}} = \dfrac{{7:7}}{{14:7}} = \dfrac{1}{3}.\)
Vậy ta nối như sau :
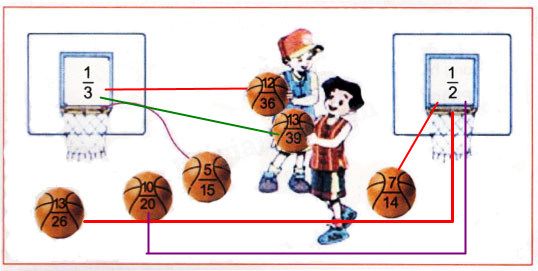
Câu 4
Quy đồng mẫu số rồi so sánh hai phân số :
a) \(\dfrac{3}{4}\) và \(\dfrac{4}{5}\) b) \(\dfrac{2}{5}\) và \(\dfrac{3}{{10}}\) c) \(\dfrac{5}{6}\) và \(\dfrac{7}{8}\)
Phương pháp giải:
- Chọn mẫu số chung (thường chọn mẫu số chung nhỏ nhất).
- Quy đồng mẫu số các phân số đã cho với mẫu số chung vừa tìm được ở trên.
- So sánh hai phân số vừa quy đồng bằng cách so sánh các tử số với nhau rồi rút ra kết luận.
Lời giải chi tiết:
a) Chọn mẫu số chung là 20.
Ta có : \(\dfrac{3}{4} = \dfrac{{3 \times 5}}{{4 \times 5}} = \dfrac{{15}}{{20}}\) và \(\dfrac{4}{5} = \dfrac{{4 \times 4}}{{5 \times 4}} = \dfrac{{16}}{{20}}\).
Mà \(\dfrac{{15}}{{20}} < \dfrac{{16}}{{20}}\) (vì 15 < 16).
Vậy \(\dfrac{3}{4} < \dfrac{4}{5}\).
b) Chọn mẫu số chung là 10.
Ta có : \(\dfrac{2}{5} = \dfrac{{2 \times 2}}{{5 \times 2}} = \dfrac{4}{{10}}\) và giữ nguyên phân số \(\dfrac{3}{{10}}\).
Mà \(\dfrac{4}{{10}} > \dfrac{3}{{10}}\) (vì 4 > 3).
Vậy \(\dfrac{2}{5} > \dfrac{3}{{10}}\).
c) Chọn mẫu số chung là 24.
Ta có : \(\dfrac{5}{6} = \dfrac{{5 \times 4}}{{6 \times 4}} = \dfrac{{20}}{{24}}\) và \(\dfrac{7}{8} = \dfrac{{7 \times 3}}{{8 \times 3}} = \dfrac{{21}}{{24}}\).
Mà \(\dfrac{{20}}{{24}} < \dfrac{{21}}{{24}}\) (vì 20 < 21).
Vậy \(\dfrac{5}{6} < \dfrac{7}{8}\).
Câu 5
Khoanh vào đồ vật tương ứng với phân số (theo mẫu):
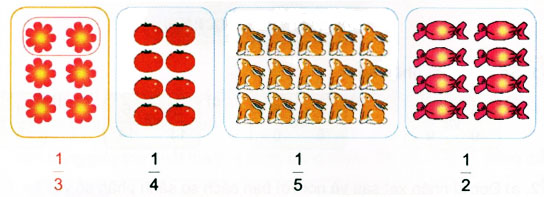
Phương pháp giải:
Hình thứ nhất gồm 6 bông hoa. Do đó \(\dfrac{1}{3}\) số bông hoa trong hình gồm 6 : 3 = 2 bông hoa.
Vậy ta khoanh vào 2 bông hoa.
Các câu khác ta làm tương tự
Lời giải chi tiết:
• Hình thứ hai có 8 quả cà chua. Do đó \(\dfrac{1}{4}\) số cà chua trong hình gồm 8 : 4 = 2 quả.
Vậy ta khoanh vào 2 quả cà chua.
• Hình thứ ba có 15 con thỏ. Do đó \(\dfrac{1}{5}\) số con thỏ trong hình gồm 15 : 5 = 3 con thỏ.
Vậy ta khoanh vào 3 con thỏ.
• Hình thứ tư có 8 cái kẹo. Do đó \(\dfrac{1}{2}\) số kẹo trong hình gồm 8 : 2 = 4 cái kẹo.
Vậy ta khoanh vào 4 cái kẹo.
Do đó ta có kết quả như sau :
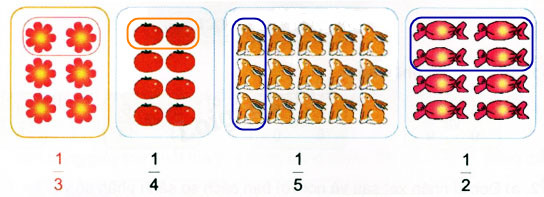
Search google: "từ khóa + timdapan.com" Ví dụ: "B. Hoạt động thực hành - Bài 70 : So sánh hai phân số cùng mẫu số timdapan.com"







