A. Hoạt động thực hành - Bài 53 : Em ôn lại những gì đã học

Câu 1

Chơi trò chơi “Tính nhẩm“ :

Mỗi nhóm chia thành hai đội nhỏ, đội 1 ra câu đố về nhân (chia) nhẩm một số với (cho) 10, 100, 1000, … Đội 2 trả lời.

Chẳng hạn : Đội 1 hỏi : 2,5 × 100. Đội 2 trả lời : 250.

Đội 1 hỏi : 346 : 10. Đội 2 trả lời : 34,6.

Hai đội đổi vai cho nhau cùng chơi.

Phương pháp giải:

Vận dụng kiến thức về phép nhân và phép chia một số với 10,100,1000… đã học, thực hiện các hoạt động.

Lời giải chi tiết:

Đội 1 hỏi : 22,2 × 10.

Đội 2 trả lời : 222.

Đội 2 hỏi : 34,5 : 100

Đội 1 trả lời : 0,345. 

Câu 2

Tính:

a) 384, 8 : 25 ;

b) 3 : 1,25 ;

c) 14,21 : 0,25.

Phương pháp giải:

Vận dụng kiến thức về phép chia một số thập phân, đặt tính rồi tính.

Lời giải chi tiết:

Câu 3

Tính giá trị biểu thức :

a) (242,7 – 60,6) × 3,2

b) 9,88 : (1,27 + 1,33) – 0,98

Phương pháp giải:

- Tính trong ngoặc trước, ngoài ngoặc sau.

- Biểu thức có phép tính nhân, chia, cộng, trừ ta tính nhân, chia trước, cộng, trừ sau.

Lời giải chi tiết:

a) (242,7 – 60,6) × 3,2               

    = 182,1 × 3,2 

    = 582,72                                     

b) 9,88 : (1,27 + 1,33) – 0,98

   = 9,88: 2,6 – 0,98

   = 3,8 – 0,98

   = 2,82

Câu 4

Tìm \(x\) biết:

a) \(x \times 100 = 46,89 + 12,7\)

b) \(59,04 : x = 5,89 - 1,09\)

Phương pháp giải:

- Muốn tìm một thừa số ta lấy tích chia cho thừa số kia.

- Muốn tìm số chia ta lấy số bị chia chia cho thương.

Lời giải chi tiết:

\(\begin{array}{l}a)\,\,\,x \times 100 = 46,89 + 12,7\\\,\,\,\,\,\,\,\,x \times 100 = 59,59\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\quad x = 59,59:100\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\quad x = 0,5959\end{array}\)

\(\begin{array}{l}b)\;59,04:x = 5,89 - 1,09\\\quad 59,04:x = 4,8\\\,\,\,\,\,\;\;\;\;\;\qquad x = 59,04:4,8\\\,\,\,\,\,\;\;\;\;\;\qquad x = 12,3\end{array}\) 

Câu 5

Giải bài toán sau:

 Trong vườn có 250 cây, gồm các loại cây cam, cây chanh và cây chuối. Số cây cam chiếm 40% và số cây chanh chiếm 30% số cây trong vườn. Hỏi trong vườn có bao nhiêu cây chuối ?

Phương pháp giải:

Cách 1 :

- Tìm tổng số phần trăm của số cây cam và số cây chanh so với số cây trong vườn.

- Tìm số cây cam và số cây chanh.

- Tìm số cây chuối.

Cách 2 :

- Tìm số cây cam : Lấy 250 chia cho 100 rồi nhân với 40.

- Tìm số cây chanh : Lấy 250 chia cho 100 rồi nhân với 30.

- Tìm số cây chuối : Lấy số cây trong vườn trừ đi số cây cam và chanh vừa tìm được.

Lời giải chi tiết:

Cách 1 :

Tỉ lệ phần trăm số cây chanh và cây cam ở trong vườn là:

            30 + 40 = 70% (số cây trong vườn)

Số cây cam và cây chanh trong vườn là:

               250 : 100 × 70 = 175 (cây)

Trong vườn có số cây chuối là:

               250 – 175 = 75 (cây)

                              Đáp số: 75 cây chuối.

Cách 2 :

Trong vườn có số cây cam là :

              250 : 100 × 40 = 100 (cây)

Trong vườn có số cây chanh là :

              250 : 100 × 30 = 75 (cây)

Trong vườn có số cây cam là :

              250 – (100 + 75) = 75 (cây)

                              Đáp số: 75 cây chuối.

Câu 6

Em hãy viết tiếp vào chỗ chấm cho thích hợp :

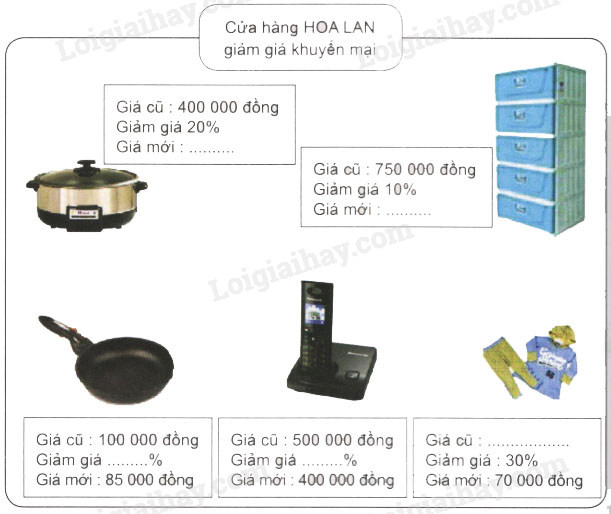
Phương pháp giải:

Dựa vào cách giải các bài toán về tỉ số phần trăm, tính rồi điền kết quả vào bảng. 

Lời giải chi tiết:

Câu 7

Khoanh vào chữ đặt trước câu trả lời đúng:

Số thích hợp để viết vào chỗ chấm của 602\({m^2}\) = .... ha là:

A. 60,2.                                      B. 6,02.

C. 0,602.                                    D. 0,0602

Phương pháp giải:

Vận dụng kiến thức : \(1ha = 10000{m^2};1{m^2} = \dfrac{1}{{10000}}ha.\)

Câu 8

Khoanh vào chữ đặt trước câu trả lời đúng

Một người gửi tiết kiệm với lãi suất 7% một năm. Sau một năm, số tiền lãi người đó nhận được là 2 100 000 đồng. Để tính số tiền gửi ban đầu của người ấy, ta cần tính :

A. 2100000 : 7

B. 2100000 × 7 : 100

C. 2100000 × 100 : 7

D. 2100000 × 7

Phương pháp giải:

Muốn tìm lời giải ta lấy số tiền lãi nhận được sau một năm chia cho 7 rồi nhân với 100 hoặc lấy số tiền lãi nhận được sau một năm nhân với 100 rồi chia cho 7.

Lời giải chi tiết:

Số tiền gửi ban đầu của người ấy là:

2 100 000 : 7 × 100 hay 2100000 × 100 : 7

Đáp án đúng là: C. 2100000 × 100 : 7.