A. Hoạt động thực hành - Bài 104 : Ôn tập về các phép tính với phân số (tiếp theo)

Câu 1

Chơi trò chơi “Ai nhanh, ai đúng ?”

a) Tính: \(\dfrac{1}{2} \times \dfrac{2}{3} \times \dfrac{3}{4} \times \dfrac{4}{5}\)                  b) Tính : \(\dfrac{4}{3}:\dfrac{5}{4}:\dfrac{6}{5}:\dfrac{7}{6}\)

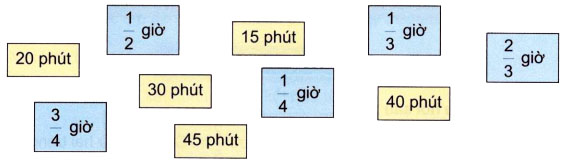
c) Tìm các cặp chỉ khoảng thời gian bằng nhau:

Phương pháp giải:

a)  Để nhân nhiều phân số ta có thể nhân các tử số với nhau, nhân các mẫu số với nhau.

b)  Để chia hai phân số ta lấy phân số thứ nhất nhân với phân số thứ hai đảo ngược.

c) Ta có 1 giờ = 60 phút nên để đổi một số từ đơn vị giờ sang phút ta lấy 60 nhân với số đó.

Lời giải chi tiết:

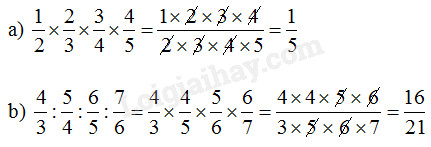
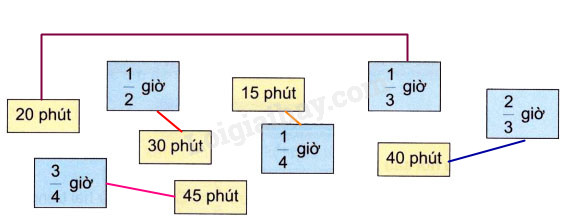
c) Ta nối như sau :

Câu 2

Phân số thứ nhất là \(\dfrac{4}{5}\) , phân số thứ hai là \(\dfrac{2}{7}\). Hãy tính tổng, hiệu, tích, thương của phân số thứ nhất và phân số thứ hai.

Phương pháp giải:

Áp dụng các quy tắc :

- Muốn cộng (hoặc trừ) hai phân số khác mẫu số ta quy đồng mẫu số hai phân số rồi cộng (hoặc trừ) hai phân số đã quy đồng mẫu số.

- Muốn nhân hai phân số ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số.

- Muốn chia hai phân số ta lấy phân số thứ nhất nhân với phân số thứ hai đảo ngược.

Lời giải chi tiết:

• Tổng : \(\dfrac{4}{5} + \dfrac{2}{7} = \dfrac{{28}}{{35}} + \dfrac{{10}}{{35}} = \dfrac{{38}}{{35}}.\)

• Hiệu : \(\dfrac{4}{5} - \dfrac{2}{7} = \dfrac{{28}}{{35}} - \dfrac{{10}}{{35}} = \dfrac{{18}}{{35}}.\)

• Tích : \(\dfrac{4}{5} \times \dfrac{2}{7} = \dfrac{{4 \times 2}}{{5 \times 7}} = \dfrac{8}{{35}}.\)

• Thương : \(\dfrac{4}{5}:\dfrac{2}{7} = \dfrac{4}{5} \times \dfrac{7}{2} = \dfrac{{28}}{{10}} = \dfrac{{14}}{5}.\)

Câu 3

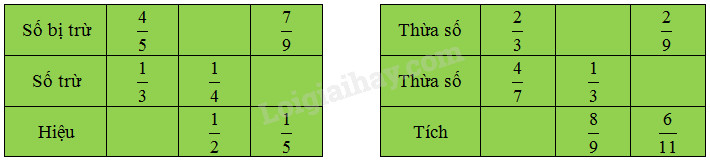
Điền số thích hợp vào ô trống :

Phương pháp giải:

Áp dụng các công thức: 

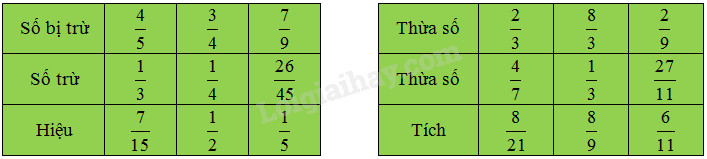
a) Số bị trừ = Hiệu + Số trừ  ;    Số trừ = Số bị trừ  – Hiệu  ;     Hiệu = Số bị trừ – Số trừ.

b) Tích = Thừa số × Thừa số  ;     Thừa số = Tích : Thừa số đã biết.

Lời giải chi tiết:

Ta có :

Vậy ta có bảng kết quả như sau :

Câu 4

Tính bằng hai cách :

\(a)\,\,\left( {\dfrac{6}{{11}} + \dfrac{5}{{11}}} \right) \times \dfrac{3}{7}\)                             \(b)\,\,\dfrac{3}{5} \times \dfrac{7}{9} + \dfrac{3}{5} \times \dfrac{2}{9}\)

\(c)\,\,\left( {\dfrac{6}{7} - \dfrac{4}{7}} \right):\dfrac{2}{5}\)                            \(d)\,\,\dfrac{8}{{15}}:\dfrac{2}{{11}} + \dfrac{7}{{15}}:\dfrac{2}{{11}}\)

Phương pháp giải:

Áp dụng các công thức :

\((a + b) × c = a × c + b × c ;\)      \((a – b) × c = a × c – b × c ;\)

\((a + b) : c = a : c +b : c ;\)      \((a – b): c = a : c – b : c.\)

Lời giải chi tiết:

a) \(\left( {\dfrac{6}{{11}} + \dfrac{5}{{11}}} \right) \times \dfrac{3}{7}\)

Cách 1: \(\left( {\dfrac{6}{{11}} + \dfrac{5}{{11}}} \right) \times \dfrac{3}{7} = \dfrac{{11}}{{11}} \times \dfrac{3}{7}\)\( = 1 \times \dfrac{3}{7} = \dfrac{3}{7}.\)

Cách 2 : \(\left( {\dfrac{6}{{11}} + \dfrac{5}{{11}}} \right) \times \dfrac{3}{7} = \dfrac{6}{{11}} \times \dfrac{3}{7} + \dfrac{5}{{11}} \times \dfrac{3}{7}\)\( = \dfrac{{18}}{{77}} + \dfrac{{15}}{{77}} = \dfrac{{33}}{{77}} = \dfrac{3}{7}.\)

b) \(\dfrac{3}{5} \times \dfrac{7}{9} + \dfrac{3}{5} \times \dfrac{2}{9}\)

Cách 1 : \(\dfrac{3}{5} \times \dfrac{7}{9} + \dfrac{3}{5} \times \dfrac{2}{9} = \dfrac{{21}}{{45}} + \dfrac{6}{{45}}\)\( = \dfrac{{27}}{{45}} = \dfrac{3}{5}.\)

Cách 2 : \(\dfrac{3}{5} \times \dfrac{7}{9} + \dfrac{3}{5} \times \dfrac{2}{9} = \dfrac{3}{5} \times \left( {\dfrac{7}{9} + \dfrac{2}{9}} \right)\)\( = \dfrac{3}{5} \times \dfrac{9}{9} = \dfrac{3}{5} \times 1 = \dfrac{3}{5}.\)

c) \(\left( {\dfrac{6}{7} - \dfrac{4}{7}} \right):\dfrac{2}{5}\)

Cách  1: \(\left( {\dfrac{6}{7} - \dfrac{4}{7}} \right):\dfrac{2}{5} = \dfrac{2}{7} \times \dfrac{5}{2}\)\( = \dfrac{{10}}{{14}} = \dfrac{5}{7}.\)

Cách 2 : \(\left( {\dfrac{6}{7} - \dfrac{4}{7}} \right):\dfrac{2}{5} = \dfrac{6}{7}:\dfrac{2}{5} - \dfrac{4}{7}:\dfrac{2}{5}\)\( = \dfrac{6}{7} \times \dfrac{5}{2} - \dfrac{4}{7} \times \dfrac{5}{2} = \dfrac{{30}}{{14}} - \dfrac{{20}}{{14}}\)\( = \dfrac{{10}}{{14}} = \dfrac{5}{7}.\)

d) \(\dfrac{8}{{15}}:\dfrac{2}{{11}} + \dfrac{7}{{15}}:\dfrac{2}{{11}}\)

Cách 1: \(\dfrac{8}{{15}}:\dfrac{2}{{11}} + \dfrac{7}{{15}}:\dfrac{2}{{11}}\)\( = \dfrac{8}{{15}} \times \dfrac{{11}}{2} + \dfrac{7}{{15}} \times \dfrac{{11}}{2}\)\( = \dfrac{{88}}{{30}} + \dfrac{{77}}{{30}} = \dfrac{{165}}{{30}} = \dfrac{{11}}{2}.\)

Cách 2 : \(\dfrac{8}{{15}}:\dfrac{2}{{11}} + \dfrac{7}{{15}}:\dfrac{2}{{11}} = \left( {\dfrac{8}{{15}} + \dfrac{7}{{15}}} \right):\dfrac{2}{{11}}\)\( = \dfrac{{15}}{{15}} \times \dfrac{{11}}{2} = 1 \times \dfrac{{11}}{2} = \dfrac{{11}}{2}.\)

Câu 5

Tính : 

\(a)\,\,\dfrac{2}{3} \times \dfrac{3}{4} \times \dfrac{4}{5}:\dfrac{1}{5}\)                                    \(b)\,\,\dfrac{2}{5} \times \dfrac{3}{4} \times \dfrac{5}{6}:\dfrac{3}{4}\)

Phương pháp giải:

- Để nhân nhiều phân số ta có thể nhân các tử số với nhau, nhân các mẫu số với nhau.

- Để chia hai phân số ta lấy phân số thứ nhất nhân với phân số thứ hai đảo ngược. 

Lời giải chi tiết:

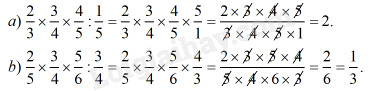
Câu 6

Một tấm vải dài 20m. Đã may quần áo hết \(\dfrac{4}{5}\) tấm vải đó. Số vải còn lại đem may các túi, mỗi túi hết \(\dfrac{2}{3}m.\) . Hỏi may được tất cả bao nhiêu cái túi như vậy ?

Phương pháp giải:

- Tìm số vải đã may quần áo ta lấy 20m nhân với \(\dfrac{4}{5}\).

- Tìm số vải còn lại ta lấy độ dài tấm vải ban đầu trừ đi số vải đã may quần áo.

- Tìm số túi may được ta lấy số vải còn lại chia cho số vải để may một cái túi.

Lời giải chi tiết:

May quần áo hết số mét vải là :

               \(20 \times \dfrac{4}{5} = \dfrac{{80}}{5} = 16\left( m \right)\)

Sau khi may quần áo, tấm vải còn số mét là :

               \(20 – 16 = 4 (m)\)

May được tất cả số cái túi là :

              \(4:\dfrac{2}{3} = 6\) (cái)

                             Đáp số: \(6\) cái túi.

Câu 7

Người ta cho một vòi nước chảy vào bể chưa có nước, mỗi giờ chảy được \(\dfrac{2}{5}\) bể.

a) Hỏi sau hai giờ vòi nước đó chảy được mấy phần bể ?

b) Nếu đã dùng hết một lượng nước bằng \(\dfrac{3}{4}\)bể thì số nước còn lại là mấy phần bể ? 

Phương pháp giải:

- Tính số nước chảy vào bể sau 2 giờ ta lấy số nước chảy vào bể sau 1 giờ nhân với 2.

- Tính số nước còn lại ta lấy số nước chảy vào bể trong 2 giờ trừ đi số nước đã dùng.

Lời giải chi tiết:

a) Sau hai giờ, vòi nước đó chảy được số phần bể là :

                \(\dfrac{2}{5} \times 2 = \dfrac{4}{5}\) (bể)

b) Nếu đã dùng một lượng nước bằng \(\dfrac{3}{4}\) bể thì số nước còn lại là :

                \(\dfrac{4}{5} - \dfrac{3}{4} = \dfrac{1}{{20}}\)  (bể)

                            Đáp số : a) \(\dfrac{4}{5}\) bể ; 

                                          b) \(\dfrac{1}{{20}}\) bể.