A. Hoạt động cơ bản - Bài 65 : Phân số bằng nhau
Giải Bài 65 : Phân số bằng nhau phần hoạt động cơ bản trang 20, 21, 22 sách VNEN toán lớp 4 với lời giải dễ hiểu
Câu 1
Chơi trò chơi "đố bạn"
- Em vẽ hình biểu diễn một phân số bất kì, chẳng hạn :

- Em đố bạn viết và đọc phân số chỉ phần đã tô màu của hình em vừa vẽ, chẳng hạn : \(\dfrac{2}{4}\) ; hai phần tư.
- Em và bạn đổi vai cùng chơi.
Phương pháp giải:
- Trong mỗi phân số, tử số chỉ số phần bằng nhau đã được tô màu và mẫu số chỉ tổng số phần bằng nhau.
- Khi đọc phân số ta đọc tử số trước, dấu gạch ngang đọc là “phần”, sau đó đọc mẫu số.
Lời giải chi tiết:
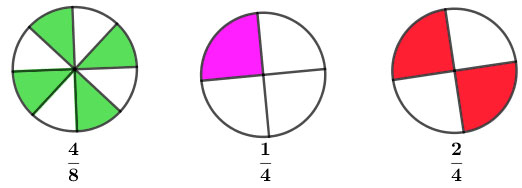
Hình 1: Phân số là \(\dfrac{4}{8}\); đọc là bốn phần tám.
Hình 2: Phân số là \(\dfrac{1}{4}\); đọc là một phần bốn.
Hình 3: Phân số là \(\dfrac{2}{4}\); đọc là hai phần bốn.
Câu 2
Thực hiện lần lượt các hoạt động sau :
a) Lấy hai băng giấy như nhau :
- Chia băng giấy thứ nhất thành 3 phần bằng nhau. Tô màu vào \(\dfrac{2}{3}\) bằng giấy.

- Chia băng giấy thứ hai thành 6 phần bằng nhau. Tô màu vào \(\dfrac{4}{6}\) bằng giấy.

b) Dán hai băng giấy vào vở rồi so sánh phần đã tô màu của hai băng giấy.
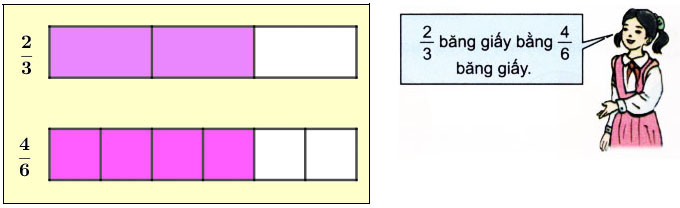
c) Đọc kĩ nội dung sau và nghe thầy/cô giáo hướng dẫn :
|
Nhận xét : \(\dfrac{2}{3} = \dfrac{{2 \times 2}}{{3 \times 2}} = \dfrac{4}{6}\) và \(\dfrac{4}{6} = \dfrac{{4:2}}{{6:2}} = \dfrac{2}{3}\) Tính chất cơ bản của phân số : - Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho. - Nếu cả tử số và mẫu số của một phân số cùng chia hết cho một số tự nhiên khác 0 thì sau khi chia ta được một phân số bằng phân số đã cho. Ví dụ : \(\dfrac{3}{4} = \dfrac{{3 \times 5}}{{4 \times 5}} = \dfrac{{15}}{{20}}\) ; \(\dfrac{{15}}{{20}} = \dfrac{{15:5}}{{20:5}} = \dfrac{3}{5}\). |
Câu 3
a) Tìm ví dụ minh họa tính chất cơ bản của phân số.
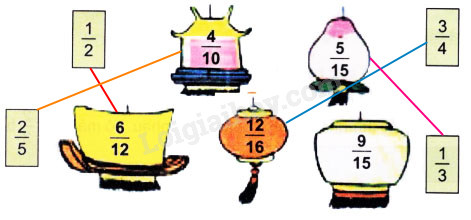
b) Chơi trò chơi “ghép thẻ” : Ghép các phân số bằng nhau :

Phương pháp giải:
Áp dụng tính chất cơ bản của phân số :
- Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.
- Nếu cả tử số và mẫu số của một phân số cùng chia hết cho một số tự nhiên khác 0 thì sau khi chia ta được một phân số bằng phân số đã cho.
Lời giải chi tiết:
a) Ví dụ :
\(\dfrac{3}{5} = \dfrac{{3 \times 4}}{{5 \times 4}} = \dfrac{{12}}{{20}}\) ; \(\dfrac{{12}}{{20}} = \dfrac{{12:4}}{{20:4}} = \dfrac{3}{5}\).
b) Ta có :
\(\dfrac{1}{2} = \dfrac{{1 \times 6}}{{2 \times 6}} = \dfrac{6}{{12}}\) ; \(\dfrac{2}{5} = \dfrac{{2 \times 2}}{{5 \times 2}} = \dfrac{4}{{10}}\) ;
\(\dfrac{3}{4} = \dfrac{{3 \times 4}}{{4 \times 4}} = \dfrac{{12}}{{16}}\) ; \(\dfrac{1}{3} = \dfrac{{1 \times 5}}{{3 \times 5}} = \dfrac{5}{{15}}\).
Vậy các thẻ được nối với nhau như sau :
Search google: "từ khóa + timdapan.com" Ví dụ: "A. Hoạt động cơ bản - Bài 65 : Phân số bằng nhau timdapan.com"







