Đề thi kì 1 môn toán lớp 8 năm 2019 - 2020 phòng GDĐT Đống Đa

Bài I.  (2,0 điểm) :  Phân tích đa thức thành nhân tử :

\(1)\;{x^2} - xy\)                 \(2)\;xy + x + y + 1\)                   \(3)\;{x^3} - 7{x^2} + 10x\)

Bài II (2,0 điểm) :

1) Rút gọn biểu thức : \(x\left( {1 - x} \right) + \left( {x + 1} \right)\left( {x - 2} \right)\)

2) Tìm \(x\) biết : \({\left( {x + 3} \right)^2} - {x^2} = 45\)

Bài III (2,0 điểm) :

Cho hai biểu thức : \(A = \dfrac{{{x^2} - 9}}{{3\left( {x + 5} \right)}}\) và \(B = \dfrac{x}{{x + 3}} + \dfrac{{2x}}{{x - 3}} - \dfrac{{3{x^2} + 9}}{{{x^2} - 9}}\) với \(x \ne  - 5;\,x \ne  \pm 3.\)

1) Tính giá trị của biểu thức \(A\) khi \(x = 2.\)

2) Rút gọn biểu thức \(B.\)

3) Cho \(P = A.B.\) Tìm giá trị nguyên của \(x\) để \(P\) có giá trị nguyên.

Bài IV. (3,5 điểm) :

Cho tam giác \(ABC\) cân tại \(A\) có đường cao \(AH\) (\(H\) thuộc \(BC\)). Gọi \(M\) là trung điểm của đoạn thẳng \(AB.\) Gọi \(E\) là điểm đối xứng với \(H\) qua \(M.\)

1) Chứng minh tứ giác \(AHBE\) là hình chữ nhật.

2) Gọi \(N\) là trung điểm của \(AH.\) Chứng minh \(N\) là trung điểm của \(EC.\)

3) Cho \(AH = 8cm;\,BC = 12cm.\) Tính diện tích tam giác \(AMH.\)

4) Trên tia đối của tia \(HA\) lấy điểm \(F.\) Kẻ \(HK \bot FC\) (\(K\) thuộc \(FC\)). Gọi \(I,\,Q\) lần lượt là trung điểm của \(HK,\,KC.\) Chứng minh rằng : \(BK \bot FI.\)

Bài V. (0,5 điểm) : Cho \(a + b + c = 0\) \(\left( {a \ne 0;\,b \ne 0;\,c \ne 0} \right).\) Tính giá trị của biểu thức

\(A = \dfrac{{{a^2}}}{{{a^2} - {b^2} - {c^2}}} + \dfrac{{{b^2}}}{{{b^2} - {c^2} - {a^2}}} \)\(+ \dfrac{{{c^2}}}{{{c^2} - {a^2} - {b^2}}}\)

----------HẾT----------

 

 

HƯỚNG DẪN GIẢI CHI TIẾT

Thực hiện: Ban chuyên môn

 

Bài I (VD):

Phương pháp:

a) Dùng phương pháp đặt nhân tử chung

b) Dùng phương pháp đặt nhân tử chung và nhóm hạng tử

c) Đặt nhân tử chung rồi tách hạng tử để nhóm các hạng tử thích hợp

Cách giải:

1) \({x^2} - xy = x\left( {x - y} \right)\)

2)

 \(\begin{array}{l}xy + x + y + 1\\ = x\left( {y + 1} \right) + \left( {y + 1} \right)\\ = \left( {y + 1} \right)\left( {x + 1} \right)\end{array}\)

3)

\(\begin{array}{l}{x^3} - 7{x^2} + 10x\\ = x\left( {{x^2} - 7x + 10} \right)\\ = x\left( {{x^2} - 2x - 5x + 10} \right)\\ = x\left[ {x\left( {x - 2} \right) - 5\left( {x - 2} \right)} \right]\\ = x\left( {x - 5} \right)\left( {x - 2} \right)\end{array}\)

Bài II (VD):

Phương pháp:

1)  Nhân đơn thức với đa thức, nhân đa thức với đa thức rồi thu gọn

2) Sử dụng hằng đẳng thức \({\left( {a + b} \right)^2} = {a^2} + 2ab + {b^2}\) sau đó rút gọn vế trái đưa về dạng tìm \(x\) thường gặp

Cách giải:

1) Rút gọn biểu thức : \(x\left( {1 - x} \right) + \left( {x + 1} \right)\left( {x - 2} \right)\)

Ta có:

\(\begin{array}{l}x\left( {1 - x} \right) + \left( {x + 1} \right)\left( {x - 2} \right)\\ = x - {x^2} + {x^2} - 2x + x - 2\\ =  - 2\end{array}\)

2) Tìm \(x\) biết : \({\left( {x + 3} \right)^2} - {x^2} = 45\)

Ta có:

\(\begin{array}{l}{\left( {x + 3} \right)^2} - {x^2} = 45\\ \Leftrightarrow {x^2} + 6x + 9 - {x^2} = 45\\ \Leftrightarrow 6x = 36\\ \Leftrightarrow x = 6\end{array}\)

Vậy \(x = 6.\)

Bài III (VD ):

Phương pháp:

1)  Thay \(x = 2\) (thỏa mãn điều kiện) vào biểu thức A rồi tính toán

2) Qui đồng mẫu các phân thức rồi cộng trừ các phân thức, sau đó rút gọn

3) Tính \(P.\) Sau đó biến đổi \(P\) về dạng \(P = a + \dfrac{b}{{f\left( x \right)}}\) với \(a,b \in Z\)

Khi đó: \(P \in Z \Rightarrow f\left( x \right) \in U\left( b \right)\), từ đó ta tìm được \(x.\)

Kết hợp điều kiện của \(x\) rồi kết luận

Cách giải:

Cho hai biểu thức : \(A = \dfrac{{{x^2} - 9}}{{3\left( {x + 5} \right)}}\) và \(B = \dfrac{x}{{x + 3}} + \dfrac{{2x}}{{x - 3}} - \dfrac{{3{x^2} + 9}}{{{x^2} - 9}}\) với \(x \ne  - 5;\,x \ne  \pm 3.\)

1) Tính giá trị của biểu thức \(A\) khi \(x = 2.\)

Với \(x = 2\) (thỏa mãn điều kiện), thay vào \(A\) ta có :

\(\begin{array}{l}A = \dfrac{{{2^2} - 9}}{{3.\left( {2 + 5} \right)}}\\A = \dfrac{{ - 5}}{{21}}\end{array}\)

Vậy  \(A =  - \dfrac{5}{{21}}\) khi \(x = 2.\)

2) Rút gọn biểu thức \(B.\)

Ta có:

\(B = \dfrac{x}{{x + 3}} + \dfrac{{2x}}{{x - 3}} - \dfrac{{3{x^2} + 9}}{{{x^2} - 9}}\)

\(\begin{array}{l}B = \dfrac{{x\left( {x - 3} \right) + 2x\left( {x + 3} \right) - 3{x^2} - 9}}{{\left( {x - 3} \right)\left( {x + 3} \right)}}\\B = \dfrac{{{x^2} - 3x + 2{x^2} + 6x - 3{x^2} - 9}}{{\left( {x - 3} \right)\left( {x + 3} \right)}}\\B = \dfrac{{3x - 9}}{{\left( {x - 3} \right)\left( {x + 3} \right)}}\\B = \dfrac{{3\left( {x - 3} \right)}}{{\left( {x - 3} \right)\left( {x + 3} \right)}}\\B = \dfrac{3}{{x + 3}}\end{array}\)

Vậy \(B = \dfrac{3}{{x + 3}}\) với \(x \ne  - 5;\,x \ne  \pm 3.\)

3) Cho \(P = A.B.\) Tìm giá trị nguyên của \(x\) để \(P\) có giá trị nguyên.

Ta có: 

\(P = A.B = \dfrac{{\left( {{x^2} - 9} \right)}}{{3\left( {x + 5} \right)}} \cdot \dfrac{3}{{x + 3}} \) \( = \dfrac{{x - 3}}{{x + 5}}= \dfrac{{x + 5 - 8}}{{x + 5}} = 1 - \dfrac{8}{{x + 5}}\)

\(P\) có giá trị nguyên thì \(\dfrac{8}{{x + 5}} \in \mathbb{Z} \)\(\Rightarrow x + 5 \in U\left( 8 \right) = \left\{ { \pm 1; \pm 2; \pm 4; \pm 8} \right\}\)

Ta có bảng sau: 

Vậy để \(P\) có giá trị nguyên thì \(x \in \left\{ { - 6; - 7; - 9; - 13; - 4; - 1} \right\}\)

Bài IV (VD ):

Phương pháp:

1) Sử dụng dấu hiệu nhận biết: “Tứ giác có hai đường chéo giao nhau tại trung điểm mỗi đường là hình bình hành” và “Hình bình hành có 1 góc vuông là hình chữ nhật”

2) Chứng minh \(AEHC\) là hình bình hành sau đó suy ra hai đường chéo \(AH,EC\) giao nhau tại trung điểm \(N\) của mỗi đường.

3) Tính diện tích tam giác \(ABH\), chứng minh \({S_{ABH}} = 2{S_{AMH}}\) từ đó ta tính được \({S_{AMH}}\)

4) Sử dụng tính chất đường trung bình của tam giác và quan hệ từ vuông góc đến song song

Cách giải:

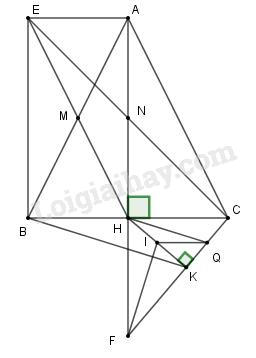
1. Chứng minh \(AHBE\) là hình chữ nhật. 

 Xét tứ giác \(AHBE\) có

\(AB \cap EH = \left\{ M \right\}\)

\(M\) là trung điểm \(AB\) (giả thiết)

\(M\) là trung điểm \(EH\) (\(E\) đối xứng với \(H\) qua \(M\))

\( \Rightarrow \) Tứ giác \(AHBE\) là hình bình hành (dấu hiệu nhận biết hình bình hành)

Mà \(\widehat {AHB} = 90^\circ \,\left( {AH \bot BC} \right)\)

\( \Rightarrow AHBE\) là hình chữ nhật (dấu hiệu nhận biết hình chữ nhật)

2. Chứng minh \(N\) là trung điểm của \(EC\)

Vì\(AHBE\) là hình chữ nhật (theo câu a)

\( \Rightarrow AE//BH;\,AE = BH\,\,\left( 1 \right)\)

Vì \(\Delta ABC\) cân tại \(A\)

\(AH\) là đường cao

\( \Rightarrow AH\) đồng thời là đường trung tuyến (tính chất tam giác cân) \( \Rightarrow HB = HC\,\,\left( 2 \right)\)

Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) \( \Rightarrow AE = HC;\,AE//HC \Rightarrow AEHC\) là hình bình hành (dấu hiệu nhận biết)

\( \Rightarrow \) Hai đường chéo \(AH\) và \(EC\) cắt nhau tại trung điểm của mỗi đường

Mà \(N\) là trung điểm \(AH\left( {gt} \right)\)

\( \Rightarrow N\) là trung điểm của \(EC\) (đpcm)

3. Cho \(AH = 8cm;\,BC = 12cm.\) Tính diện tích tam giác \(AMH.\)

Ta có \(HB = HC = \dfrac{{BC}}{2} = 6cm\)

Tam giác \(ABH\) vuông tại \(H\) nên \({S_{ABH}} = \dfrac{1}{2}AH.HB = \dfrac{1}{2} \cdot 8 \cdot 6 = 24c{m^2}\)

Tam giác \(HAB\) và tam giác \(HMA\) có cùng chiều cao hạ từ đỉnh \(H\)và  cạnh đáy \(AB\) gấp hai lần cạnh đáy \(MA\) nên \({S_{ABH}} = 2{S_{AMH}}\) 

Suy ra \({S_{AMH}} = \dfrac{1}{2}{S_{ABH}} = \dfrac{1}{2}.24 = 12c{m^2}\)

Vậy \({S_{AMH}} = 12c{m^2}\)

4. Trên tia đối của tia \(HA\) lấy điểm \(F.\) Kẻ \(HK \bot FC\) (\(K\) thuộc \(FC\)). Gọi \(I,\,Q\) lần lượt là trung điểm của \(HK,\,KC.\) Chứng minh rằng : \(BK \bot FI.\)

Xét tam giác \(HKC\) có \(I,Q\) lần lượt là trung điểm cạnh \(HK,CQ\) nên \(IQ\) là đường trung bình \(\Delta HKC\)

\( \Rightarrow IQ//HC\)  (tính chất)

Mà  \(HC \bot HF\) \( \Rightarrow IQ \bot HF\)

Xét tam giác \(HFQ\) có \(IQ \bot HF\left( {cmt} \right),\,HK \bot FQ\left( {gt} \right)\) mà \(I \in HK \Rightarrow \)\(I\) là trực tâm của \(\Delta HFQ\)

\( \Rightarrow FI \bot HQ\)

Xét tam giác \(BCK\) có \(H,Q\) lần lượt là trung điểm cạnh \(BC,CQ\) nên \(HQ\) là đường trung bình \(\Delta BCK\)

\( \Rightarrow HQ//BK\) mà \(FI \bot HQ\left( {cmt} \right)\)

\( \Rightarrow BK \bot FI\) (đpcm)

Bài V (VDC ): 

Phương pháp:

Sử dụng hằng đẳng thức \({\left( {x + y} \right)^2} = {x^2} + 2xy + {y^2}\)

Biến đổi để có \(A = \dfrac{{{a^3} + {b^3} + {c^3}}}{{2abc}}\)

Sau đó chứng minh \({a^3} + {b^3} + {c^3} = 3abc\), từ đó ta tính được \(A.\)

Cách giải:

Vì \(a + b + c = 0\) nên \(a =  - b - c \Rightarrow {a^2} = {\left( { - b - c} \right)^2}\) \( \Rightarrow {a^2} = {b^2} + 2bc + {c^2}\)

\( \Rightarrow {a^2} - {b^2} - {c^2} = 2bc\)

Tương tự ta có: \({b^2} - {a^2} - {c^2} = 2ac;\,\)\({c^2} - {b^2} - {a^2} = 2ab\)

Khi đó:

\(A = \dfrac{{{a^2}}}{{2bc}} + \dfrac{{{b^2}}}{{2ac}} + \dfrac{{{c^2}}}{{2ab}} \)\(= \dfrac{{{a^3} + {b^3} + {c^3}}}{{2abc}}\)

Vì \(a + b + c = 0\) nên \(a + b =  - c\)

\(\begin{array}{l} \Leftrightarrow {\left( {a + b} \right)^3} =  - {c^3}\\ \Leftrightarrow {a^3} + {b^3} + 3ab\left( {a + b} \right) + {c^3} = 0\\ \Leftrightarrow {a^3} + {b^3} + {c^3} =  - 3ab.\left( { - c} \right)\\ \Leftrightarrow {a^3} + {b^3} + {c^3} = 3abc\end{array}\)

Từ đó:

\(A = \dfrac{{{a^3} + {b^3} + {c^3}}}{{2abc}} = \dfrac{{3abc}}{{2abc}} = \dfrac{3}{2}\)

Vậy \(A = \dfrac{3}{2}.\)

Hết