Giải đề thi học kì 2 toán lớp 11 năm 2019 - 2020 Sở GD&ĐT Bắc Ninh

Câu 1  (3,0 điểm):

Tính các giới hạn sau đây:

a) \(\mathop {\lim }\limits_{x \to 3} \left( {{x^3} - 2x + 1} \right)\)

b) \(\mathop {\lim }\limits_{x \to 2} \frac{{{x^2} - 10x + 16}}{{x - 2}}\)

c) \(\lim \frac{{2{n^2} + n - 1}}{{5 - n}}\)

Câu 2 (2,5 điểm):

Cho hàm số \(y = 2{x^2} - 3x + 1\) có đồ thị là parabol (P).

a) Tính đạo hàm \(y'\) của hàm số đã cho và giải phương trình \(y' = 0\).

b) Viết phương trình tiếp tuyến của parabol \(\left( P \right)\) tại điểm có hoành độ \({x_0} =  - 1\).

Câu 3 (3,5 điểm):

Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(AB = a,AD = a\sqrt 2 \), đường thẳng \(SA\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\), \(SA = a\sqrt 3 \) (với \(a > 0\)). Gọi \(M,N\) lần lượt là các điểm thuộc đường thẳng \(SB,SD\) sao cho \(AM\) vuông góc với \(SB\) và \(AN\) vuông góc với \(SD\). Gọi \(I\) là trung điểm của đoạn thẳng \(MN\) và \(H\) là trung điểm của đoạn thẳng \(SC\).

a) Chứng minh rằng đường thẳng \(CD\) vuông góc với mặt phẳng \(\left( {SAD} \right)\) và đường thẳng \(AN\) vuông góc với mặt phẳng \(\left( {SCD} \right)\).

b) Gọi góc giữa đường thẳng \(AC\) và mặt phẳng \(\left( {SCD} \right)\) là \(\varphi \). Tính \(\sin \varphi \).

c) Tính độ dài đoạn thẳng \(IH\) theo \(a\).

Câu 4 (1,0 điểm):

Cho các số thực \(a,b,c\) thỏa mãn điều kiện \(7a + b + 3c = 0\). Chứng minh rằng phương trình \(a{x^2} + bx + c = 2020\cos \frac{{\pi x}}{2}\) có ít nhất một nghiệm trên \(\mathbb{R}\).

HẾT

HƯỚNG DẪN GIẢI CHI TIẾT

Thực hiện: Ban chuyên môn

Câu 1 (VD):

Phương pháp:

a) Thay \(x = 3\) vào hàm số dưới dấu giới hạn.

b) Khử dạng vô định bằng cách phân tích tử thành nhân tử.

c) Chia cả tử và mẫu cho \(n\) và áp dụng quy tắc tính giới hạn.

Cách giải:

Tính các giới hạn sau đây:

a) \(\mathop {\lim }\limits_{x \to 3} \left( {{x^3} - 2x + 1} \right)\)

\(\mathop {\lim }\limits_{x \to 3} \left( {{x^3} - 2x + 1} \right)\) \( = {3^3} - 2.3 + 1 = 22\)

b) \(\mathop {\lim }\limits_{x \to 2} \frac{{{x^2} - 10x + 16}}{{x - 2}}\)

\(\begin{array}{l}\mathop {\lim }\limits_{x \to 2} \frac{{{x^2} - 10x + 16}}{{x - 2}}\\ = \mathop {\lim }\limits_{x \to 2} \frac{{\left( {x - 2} \right)\left( {x - 8} \right)}}{{x - 2}}\\ = \mathop {\lim }\limits_{x \to 2} \left( {x - 8} \right)\\ = 2 - 8\\ = 6\end{array}\)

c) \(\lim \frac{{2{n^2} + n - 1}}{{5 - n}}\)

\(\begin{array}{l}\lim \frac{{2{n^2} + n - 1}}{{5 - n}}\\ = \lim \frac{{{n^2}\left( {2 + \frac{1}{n} - \frac{1}{{{n^2}}}} \right)}}{{n\left( {\frac{5}{n} - 1} \right)}}\\ = \lim \left[ {n.\frac{{2 + \frac{1}{n} - \frac{1}{{{n^2}}}}}{{\frac{5}{n} - 1}}} \right]\\ =  - \infty \end{array}\)

Vì \(\lim n =  + \infty \) và \(\lim \frac{{2 + \frac{1}{n} - \frac{1}{{{n^2}}}}}{{\frac{5}{n} - 1}}\) \( = \frac{{2 + 0 - 0}}{{0 - 1}} =  - 2 < 0\).

Câu 2 (VD):

Phương pháp:

a) Sử dụng công thức \(\left( {{x^n}} \right)' = n{x^{n - 1}}\) tính \(y'\).

b) Phương trình tiếp tuyến với đồ thị hàm số \(y = f\left( x \right)\) tại điểm \({M_0}\left( {{x_0};{y_0}} \right)\) là:

\(y = f'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + {y_0}\)

Cách giải:

Cho hàm số \(y = 2{x^2} - 3x + 1\) có đồ thị là parabol (P).

a) Tính đạo hàm \(y'\) của hàm số đã cho và giải phương trình \(y' = 0\).

\(\begin{array}{l}y' = \left( {2{x^2}} \right)' - \left( {3x} \right)' + \left( 1 \right)'\\ = 2.2x - 3.1 + 0\\ = 4x - 3\\y' = 0 \Leftrightarrow 4x - 3 = 0\\ \Leftrightarrow 4x = 3\\ \Leftrightarrow x = \frac{3}{4}\end{array}\)

Vậy với \(x = \frac{3}{4}\) thì \(y' = 0\).

b) Viết phương trình tiếp tuyến của parabol \(\left( P \right)\) tại điểm có hoành độ \({x_0} =  - 1\).

Đặt \(y = f\left( x \right) = 2{x^2} - 3x + 1\).

Với \({x_0} =  - 1\) thì \({y_0} = f\left( { - 1} \right)\) \( = 2.{\left( { - 1} \right)^2} - 3.\left( { - 1} \right) + 1 = 6\)

Hệ số góc của tiếp tuyến: \(k = f'\left( { - 1} \right) = 4.\left( { - 1} \right) - 3 =  - 7\)

Phương trình tiếp tuyến: \(y =  - 7\left( {x + 1} \right) + 6\) hay \(y =  - 7x - 1\).

Câu 3 (VD):

Phương pháp:

a) Muốn chứng minh \(d \bot \left( P \right)\) ta chứng minh \(d\) vuông góc với hai đường thẳng cắt nhau nằm trong \(\left( P \right)\)

b) Góc giữa đường thẳng \(d\) và mặt phẳng \(\left( P \right)\) là góc giữa đường thẳng \(d\) và \(d'\) với \(d'\) là hình chiếu của \(d\) lên mặt phẳng \(\left( P \right)\).

Tính toán theo định lý Pytago và tỉ số lượng giác của góc nhọn

c) Sử dụng qui tắc cộng trừ các véc tơ để biểu diễn được \(\overrightarrow {IH} \) theo \(\overrightarrow {SA} ,\overrightarrow {AB} ,\overrightarrow {AD} \)

Từ đó sử dụng tích vô hướng của hai véc tơ bằng \(0\) nếu giá của chúng vuông góc với nhau để tính độ dài \(IH.\)

Cách giải:

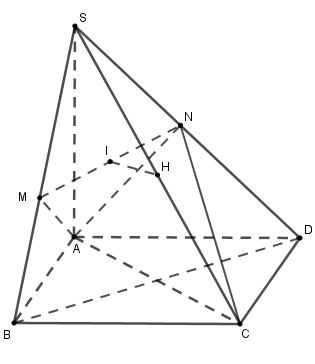
a) Chứng minh rằng đường thẳng \(CD\) vuông góc với mặt phẳng \(\left( {SAD} \right)\) và đường thẳng \(AN\) vuông góc với mặt phẳng \(\left( {SCD} \right)\).

Vì \(ABCD\) là hình chữ nhật nên \(CD \bot AD\)

Vì \(SA \bot \left( {ABCD} \right)\) \( \Rightarrow SA \bot CD\)

Ta có:  \(\left\{ \begin{array}{l}CD \bot AD\\CD \bot SA\\AD \cap SA = \left\{ A \right\}\end{array} \right.\) \( \Rightarrow CD \bot \left( {SAD} \right)\)

Vì \(\left\{ \begin{array}{l}CD \bot \left( {SAD} \right)\\AN \subset \left( {SAD} \right)\end{array} \right.\) \( \Rightarrow CD \bot AN\)

Ta có: \(\left\{ \begin{array}{l}AN \bot SD\\AN \bot CD\\SD \cap CD = \left\{ D \right\}\end{array} \right.\) \( \Rightarrow AN \bot \left( {SCD} \right)\)                   

 b) Gọi góc giữa đường thẳng \(AC\) và mặt phẳng \(\left( {SCD} \right)\) là \(\varphi \). Tính \(\sin \varphi \).

Ta có \(AN \bot \left( {SCD} \right)\) tại \(N\) (cmt) nên \(CN\) là hình chiếu của \(CA\) lên mặt phẳng \(\left( {SCD} \right)\)

Suy ra góc giữa \(AC\) và \(\left( {SCD} \right)\) là góc giữa \(CA\) và \(CN\). Hay \(\varphi  = \widehat {ACN}\).

Ta tính \(\widehat {ACN}\) .

Vì \(SA \bot \left( {ABCD} \right)\) nên \(SA \bot AC\)

Xét tam giác \(SAC\) vuông tại \(A,\) theo hệ thức lượng trong tam giác vuông ta có:

\(\frac{1}{{A{N^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{D^2}}}\) \( \Leftrightarrow \frac{1}{{A{N^2}}} = \frac{1}{{3{a^2}}} + \frac{1}{{2{a^2}}}\) \( = \frac{5}{{6{a^2}}}\) \( \Rightarrow AN = \frac{{\sqrt {30} }}{5}\)

Xét tam giác \(ABC\) vuông tại \(B\), theo định lý Pytago ta có: \(AC = \sqrt {A{B^2} + B{C^2}} \) \( = \sqrt {{a^2} + {{\left( {a\sqrt 2 } \right)}^2}}  = a\sqrt 3 \)

Vì \(AN \bot \left( {SCD} \right)\) mà \(CN \subset \left( {SCD} \right)\) nên \(AN \bot CN\)

Xét tam giác vuông \(ANC\) có \(\sin \widehat {ACN} = \frac{{AN}}{{AC}}\) \( = \frac{{\frac{{a\sqrt {30} }}{5}}}{{a\sqrt 3 }} = \frac{{\sqrt {10} }}{5}\)

Suy ra \(\sin \varphi  = \frac{{\sqrt {10} }}{5}\).

c) Tính độ dài đoạn thẳng \(IH\) theo \(a\).

Vì \(\Delta SAD,\Delta SAB\) vuông tại \(A\) nên \(N,M\) lần lượt thuộc đoạn \(SB,SD\).

Xét tam giác \(SAD\) vuông tại \(A\) có \(S{A^2} = SN.SD\) \( \Leftrightarrow \frac{{SN}}{{SD}} = \frac{{S{A^2}}}{{S{D^2}}}\) \( = \frac{{S{A^2}}}{{S{A^2} + A{D^2}}}\) \( = \frac{{3{a^2}}}{{3{a^2} + 2{a^2}}} = \frac{3}{5}\)

Suy ra \(\overrightarrow {SN}  = \frac{3}{5}\overrightarrow {SD} \)

Xét tam giác \(SAB\) vuông tại \(A\) có \(S{A^2} = SM.SB\) \( \Leftrightarrow \frac{{SM}}{{SB}} = \frac{{S{A^2}}}{{S{B^2}}}\) \( = \frac{{3{a^2}}}{{3{a^2} + {a^2}}} = \frac{3}{4}\)

Suy ra \(\overrightarrow {SM}  = \frac{3}{4}\overrightarrow {SB} \)

Ta có: \(\overrightarrow {IH}  = \overrightarrow {SH}  - \overrightarrow {SI} \)

\( = \frac{1}{2}\overrightarrow {SC}  - \frac{1}{2}\left( {\overrightarrow {SM}  + \overrightarrow {SN} } \right)\)

\( = \frac{1}{2}\overrightarrow {SC}  - \frac{1}{2}\left( {\frac{3}{4}\overrightarrow {SB}  + \frac{3}{5}\overrightarrow {SD} } \right)\)

\( = \frac{1}{2}\overrightarrow {SC}  - \frac{3}{8}\overrightarrow {SB}  - \frac{3}{{10}}\overrightarrow {SD} \)  

\( = \frac{1}{2}\left( {\overrightarrow {SA}  + \overrightarrow {AC} } \right) - \frac{3}{8}\left( {\overrightarrow {SA}  + \overrightarrow {AB} } \right)\)\(- \frac{3}{{10}}\left( {\overrightarrow {SA}  + \overrightarrow {AD} } \right)\)

\( = \frac{1}{2}\left( {\overrightarrow {SA}  + \overrightarrow {AB}  + \overrightarrow {AD} } \right) \)\(- \frac{3}{8}\left( {\overrightarrow {SA}  + \overrightarrow {AB} } \right)\)\( - \frac{3}{{10}}\left( {\overrightarrow {SA}  + \overrightarrow {AD} } \right)\)

\( =  - \frac{7}{{40}}\overrightarrow {SA}  + \frac{1}{8}\overrightarrow {AB}  + \frac{1}{5}\overrightarrow {AD} \)

Vì \(SA,AB,AD\) đôi một vuông góc nên ta có:

\(I{H^2} = {\left( { - \frac{7}{{40}}\overrightarrow {SA}  + \frac{1}{8}\overrightarrow {AB}  + \frac{1}{5}\overrightarrow {AD} } \right)^2}\)

\( = {\left( {\frac{7}{{40}}} \right)^2}{\overrightarrow {SA} ^2} + \frac{1}{{64}}{\overrightarrow {AB} ^2} + \frac{1}{{25}}{\overrightarrow {AD} ^2}\) \( - 2.\frac{7}{{40}}.\frac{1}{8}.\overrightarrow {SA} .\overrightarrow {AB} \) \( - 2.\frac{7}{{40}}.\frac{1}{5}.\overrightarrow {SA} .\overrightarrow {AD} \)\( + 2.\frac{1}{5}.\frac{1}{8}.\overrightarrow {AD} .\overrightarrow {AB} \)

\( = {\left( {\frac{7}{{40}}} \right)^2}S{A^2} + \frac{1}{{64}}A{B^2} + \frac{1}{{25}}A{D^2}\)

\( = {\left( {\frac{7}{{40}}} \right)^2}.3{a^2} + \frac{1}{{64}}{a^2} + \frac{1}{{25}}.2{a^2}\)

=\(\frac{3}{{16}}{a^2}\)

Vậy \(IH = \frac{{a\sqrt 3 }}{4}\).

Câu 4 (VDC):

Phương pháp:

Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên \(\left( {a,b} \right)\)

Nếu ta có \(f\left( a \right).f\left( b \right) < 0\) thì phương trình \(f\left( x \right) = 0\) có ít nhất 1 nghiệm \({x_0} \in \left( {a;b} \right)\)

Cách giải:

Cho các số thực \(a,b,c\) thỏa mãn điều kiện \(7a + b + 3c = 0\). Chứng minh rằng phương trình \(a{x^2} + bx + c = 2020\cos \frac{{\pi x}}{2}\) có ít nhất một nghiệm trên \(\mathbb{R}\). 

Xét hàm số \(f\left( x \right) = a{x^2} + bx + c - 2020\cos \frac{{\pi x}}{2}\) xác định và liên tục trên \(\mathbb{R}.\)

Ta có: \(f\left( 1 \right) = a + b + c\)

\(f\left( { - 1} \right) = a - b + c\)

\(f\left( 3 \right) = 9a + 3b + c\)

Suy ra \(2f\left( 1 \right) + f\left( 3 \right) + 3f\left( { - 1} \right)\) \( = 2a + 2b + 2c\) \( + 9a + 3b + c\) \( + 3a - 3b + 3c\)

\( = 14a + 2b + 6c\) \( = 2.\left( {7a + b + 3c} \right) = 0\)

Hay \(2f\left( 1 \right) + f\left( 3 \right) + 3f\left( { - 1} \right) = 0\)

+) Nếu trong ba số \(f\left( 1 \right);f\left( { - 1} \right);f\left( 3 \right)\) có 1 số bằng \(0\) thì hai số còn lại có tổng bằng 0 nên chúng trái dấu.

Suy ra phương trình \(f\left( x \right) = 0\) luôn có ít nhất 1 nghiệm

+) Nếu cả 3 số  \(f\left( 1 \right);f\left( { - 1} \right);f\left( 3 \right)\) đều khác 0, vì \(2f\left( 1 \right) + f\left( 3 \right) + 3f\left( { - 1} \right) = 0\) nên trong ba số  \(f\left( 1 \right);f\left( { - 1} \right);f\left( 3 \right)\)chắc chắn có hai số trái dấu nhau.

Suy ra phương trình \(f\left( x \right) = 0\) luôn có ít nhất 1 nghiệm

Vậy với \(7a + b + 3c = 0\) thì phương trình \(a{x^2} + bx + c = 2020\cos \frac{{\pi x}}{2}\) có ít nhất một nghiệm trên \(\mathbb{R}\).

HẾT