Giải đề thi học kì 2 lý lớp 11 năm 2019 - 2020 trường THPT B Nghĩa Hưng

Đề bài

I.TRẮC NGHIỆM (4 điểm)

Câu 1: Đặt vật AB trước thấu kính phân kỳ, ta được ảnh A’B’. Đưa vật ra xa thấu kính thêm 30 cm thì ảnh tịnh tiến 1 cm. Ảnh trước cao gấp 1,2 lần sau. Tiêu cự của thấu kính là

A.-30 cm                     B. -40 cm 

C. -10 cm                    D. -20 cm

Câu 2: Qua lăng kính có chiết suất lớn hơn chiết suất môi trường, ánh sáng đơn sắc bị lệch về phía

A.trên của lăng kính

B. dưới của lăng kính

C. cạnh của lăng kính 

D. đáy của lăng kính  

Câu 3: Một người sử dụng kính thiên văn để ngắm chừng ở vô cực. Vật kính có tiêu cự 1 m, vật kính và thị kính cách nhau 104 cm. Số bội giác của kính là:

A.10                            B. 15 

C. 25                           D. 10,4           

Câu 4: Công thức trong trường hợp nào sau đây là công thức về số bội giác của kính thiên văn trong trường hợp ngắm chừng ở vô cực?

A.\({G_\infty } = {f_1}{f_2}\)       B. \({G_\infty } = \frac{{{f_1}}}{{{f_2}}}\)     

C. \({G_\infty } = \frac{{{f_2}}}{{{f_1}}}\)         D. \({G_\infty } = \frac{{\delta D}}{{{f_1}{f_2}}}\)

Câu 5: Qua thấu kính hội tụ, nếu vật thật cho ảnh ảo thì vật phải nằm trước kính một khoảng

A.lớn hơn 2f               B. bằng 2f 

C. từ 0 đến f               D. từ f đến 2f

Câu 6: Vật sáng AB đặt vuông góc với trục chính của một thấu kính cách thấu kính 20 cm, qua thấu kính cho một ảnh thật cao gấp 5 lần vật. Khoảng cách từ vật đến ảnh là

A.20 cm                      B. 80 cm 

C. 120 cm                   D.16 cm

Câu 7: Tia tới song song với trục chính của thấu kính hội tụ có tia ló

A.đi qua quang tâm 

B. đi qua tiêu điểm ảnh chính

C. truyền thẳng 

D. phản xạ ngược trở lại

Câu 8: Lăng kính phản xạ toàn phần là một khối lăng trụ thủy tinh có tiết diện thẳng là

A.một tam giác đều 

B. một tam giác vuông cân    

C. một tam giác bất kì  

D. một hình vuông

Câu 9: Chiếu ánh sáng từ không khí vào nước có chiết suất \(n = \frac{4}{3}\). Nếu góc khúc xạ r là 30⁰ thì góc tới i (lấy tròn) là:

A. 20⁰                          B. 36⁰  

C. 42⁰                          D. 45⁰

Câu 10: Trên vành kính lúp có ghi x10, tiêu cự của kính là

A.f = 2,5 cm                B. f = 10 m 

C. f = 10 cm                D. f = 2,5 m

Câu 11: Chiếu chùm tia sáng hẹp đơn sắc từ không khí vào một môi trường trong suốt với góc tới i thì thấy tia khúc xạ vuông góc với tia phản xạ. Chiết suất n của môi trường đó đối với ánh sáng chiếu vào được xác định bởi

A.\(\sin i\)                    B. \(\cos i\) 

C. \(\frac{1}{{\sin i}}\)                    D. \(\tan i\)

Câu 12: Thấu kính hội tụ có tiêu cự f. Khoảng cách ngắn nhất giữa vật thật và ảnh thật qua thấu kính là

A.4f                             B. 3f  

C. 5f                            D. 6f

Câu 13: Hiện tượng khúc xạ ánh sáng là hiện tượng ánh sáng bị

A. giảm cường độ khi truyền qua mặt phân cách giữa hai môi trường trong suốt

B. đổi màu sắc khi truyền qua mặt phân cách giữa hai môi trường trong suốt

C. phản xạ khi truyền tới mặt phân cách giữa hai môi trường trong suốt

D. gãy khúc khi truyền xiên góc qua mặt phân cách giữa hai môi trường trong suốt

Câu 14: Vật sáng AB đặt vuông góc với trục chính của một thấu kính có tiêu cự f = 30 cm. Qua thấu kính vật cho một ảnh thật có chiều cao gấp 2 lần vật. Khoảng cách từ vật đến thấu kính là

A.45 cm                      B. 30 cm  

C. 60 cm                     D. 20 cm

Câu 15: Trong giờ thực hành môn Sinh học, để quan sát những tế bào thì các bạn học sinh phải dùng

A.kính cận                    B. kính hiển vi 

C. kính thiên văn          D. kính lúp

Câu 16: Chiếu một chùm sáng đơn sắc song song có dạng một dải mỏng và có bề rộng 10mm từ không khí vào bề mặt của một chất lỏng có chiết suất n = 1,5 với góc tới 45⁰. Dải sáng nằm trong một mặt phẳng vuông góc với mặt thoáng của chất lỏng. Bề rộng của dải tia sáng khi nó truyền trong chất lỏng là:

A.9,42 mm                  B. 14,14 mm

C. 4,71 mm                 D. 12,47 mm

II. TỰ LUẬN (6 điểm)

Câu 1: Một cái máng nước sâu 30 cm rộng 40 cm, có hai thành bên thẳng đứng. Lúc máng cạn nước thì bóng râm của thành A kéo dài tới đúng chân thành B đối diện. Người ta đổ nước vào máng đến độ cao h bằng 2/3 độ cao của thành thì bóng của thành A ngắn bớt đi một đoạn d so với trước. Biết chiết suất của nước là n = 4/3. Xác định d.

 Câu 2: Một thấu kính hội tụ có tiêu cự f = 20 cm. 

a) Xác định độ tụ của thấu kính.

b) Một vật sáng AB đặt vuông góc với trục chính của thấu kính, cách thấu kính một đoạn 30 cm, A thuộc trục chính. Xác định vị trí ảnh, số phóng đại ảnh và vẽ ảnh đúng tỉ lệ. 

c) Tại vị trí ảnh trên người ta đặt một màn ảnh song song với vật, sau đó dịch chuyển vật ra xa thấu kính một đoạn 8 cm thì phải di chuyển thấu kính về vị trí nào để tiếp tục thu được ảnh hiện rõ trên màn, và di chuyển một đoạn bằng bao nhiêu? 

Lời giải chi tiết

HƯỚNG DẪN GIẢI CHI TIẾT

THỰC HIỆN: BAN CHUYÊN MÔN LOIGIAIHAY.COM

I.TRẮC NGHIỆM

1.A	2.D	3.C	4.B	5.C	6.C	7.B	8.B
9.C	10.A	11.D	12.A	13.D	14.A	15.B	16.D

Câu 1:

Phương pháp

Sử dụng các công thức: \(\left\{ \begin{array}{l}\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\\k =  - \frac{{d'}}{d}\end{array} \right.\)

Cách giải

Ta có: \(\left\{ \begin{array}{l}\frac{1}{f} = \frac{1}{d} - \frac{1}{{d'}} \Rightarrow d' = \frac{{df}}{{d + f}}\left( 1 \right)\\\frac{1}{f} = \frac{1}{{d' + 1}} - \frac{1}{{d + 30}} \Rightarrow d' + 1 = \frac{{\left( {d + 30} \right)f}}{{d + 30 + f}}\left( 2 \right)\end{array} \right.\)

Vì ảnh trước gấp 1,2 lần ảnh sau nên ta có:

\(\left\{ \begin{array}{l}{k_1} = \frac{{d'}}{d} = \frac{f}{{d + f}}\\{k_2} = \frac{{d' + 1}}{{d + 30}} = \frac{f}{{d + 30 + f}}\end{array} \right.\\ \Rightarrow \frac{{{k_1}}}{{{k_2}}} = \frac{{d + 30 + f}}{{d + f}} = 1,2 \Leftrightarrow d + f = 150\) (3)

Từ (1),(2),(3) ta được phương trình:

\(\frac{{\left( {150 - f} \right)f}}{{150}} + 1 = \frac{{\left( {150 - f + 30} \right)f}}{{150 + 30}} \Leftrightarrow f = 30cm\)

Chọn A

Câu 2:

Phương pháp

Sử dụng lý thuyết lăng kính.

Cách giải

Ánh sáng qua lăng kính đều bị lệch về phí đáy của lăng kính.

Chọn D

Câu 3:

Phương pháp

Sử dụng biểu thức xác định độ bội giác: \({G_\infty } = \frac{{{f_1}}}{{{f_2}}}\)

Cách giải

Ta có:

+ Tiêu cự của vật kính \({f_1} = 1m = 100cm\)

+ Khoảng cách giữa vật kính và thị kính là\({f_1} + {f_2} = 104cm\)

Suy ra tiêu cự của thị kính là: \({f_2} = 104 - {f_1} = 104 - 100 = 4cm\)

Số bội giác của kính là:

\({G_\infty } = \frac{{{f_1}}}{{{f_2}}} = \frac{{100}}{4} = 25\)

Chọn C

Câu 4:

Phương pháp

Sử dụng lý thuyết kính thiên văn.

Cách giải

Sử dụng biểu thức xác định độ bội giác của kính thiên văn là: \({G_\infty } = \frac{{{f_1}}}{{{f_2}}}\)

Chọn  B

Câu 5:

Phương pháp

Sử dụng lý thuyết ảnh của vật tạo bởi thấu kính hội tụ.

Cách giải

Qua thấu kính hội tụ, nếu vật thật cho ảnh ảo thì vật phải nằm trước thấu kính một khoảng từ 0 đến f.

Chọn C

Câu 6:

Phương pháp

Sử dụng các công thức \(\left\{ \begin{array}{l}L = d + d'\\k =  - \frac{{d'}}{d}\end{array} \right.\)

Cách giải

Ta có:

Qua thấu kính cho ảnh thật => d’ > 0 => k < 0

Ảnh thật cao gấp 5 lần vật suy ra \(k =  - \frac{{d'}}{d} =  - 5 \Leftrightarrow d' = 5{\rm{d =  5}}{\rm{.20 = 100cm}}\)

Khoảng cách từ vật đến ảnh \(L = d + d' = 20 + 100 = 120cm\)

Vật sáng AB đặt vuông góc với trục chính của một thấu kính cách thấu kính 20 cm, qua thấu kính cho một ảnh thật cao gấp 5 lần vật. Khoảng cách từ vật đến ảnh là

Chọn C

Câu 7:

Phương pháp

Sử dụng lý thuyết đặc điểm đường truyền của ba tia sáng đặc biệt qua tháu kính hội tụ:

+ Tia tới đến quang tâm thì tia ló tiếp tục truyền thẳng theo phương của tia tới.

+ Tia tới song song với trục chính thì tia ló qua tiêu điểm ảnh chính.

+ Tia tới qua tiêu điểm thì tia ló song song với trục chính.

Cách giải

Tia tới song song với trục chính của thấu kính hội tụ có tia ló đi qua tiêu điểm ảnh chính.

Chọn B

Câu 8:

Phương pháp

Sử dụng lý thuyết lăng kính phản xạ toàn phần.

Cách giải

Lăng kính phản xạ toàn phần là lăng kính thủy tinh có tiết diện thẳng là một tam giác vuông cân.

Chọn B

Câu 9:

Phương pháp

Sử dụng biểu thức định luật khúc xạ ánh sáng: \({n_1}\sin i = {n_2}\sin r\)

Cách giải

Ta có:

\({n_1}\sin i = {n_2}\sin r \\\Leftrightarrow \sin i = \frac{{{n_2}\sin r}}{{{n_1}}} = \frac{4}{3}.\sin {30^0} = \frac{2}{3}\)

\( \Rightarrow i = {42^0}\)

Chọn C

Câu 10:

Phương pháp

Sử dụng công thức số bội giác của kính lúp \({G_\infty } = \frac{{25}}{f}\)

Cách giải

Trên vành kính lúp có ghi x10, tiêu cự của kính là \(\frac{{25}}{{10}} = 2,5cm\)

Chọn A

Câu 11:

Phương pháp

Sử dụng biểu thức định luật khúc xạ ánh sáng.

Sử dụng môi quan hệ giữa các góc lượng giác.

Cách giải

Ta có:

\(\left\{ \begin{array}{l}\sin i = n\sin r\\i + r = {90^0} \Rightarrow r = {90^0} - i\end{array} \right. \\\Rightarrow \sin i = n\sin \left( {{{90}^0} - i} \right) = n.\cos i\)

\( \Rightarrow \frac{{\sin i}}{{\cos i}} = n \Leftrightarrow \tan i = n\)

Chọn D

Câu 12:

Phương pháp

Sử dụng các công thức: \(\left\{ \begin{array}{l}L = d + d'\\d' = \frac{{df}}{{d - f}}\end{array} \right.\)

Cách giải

Khoảng cách giữa vật thật và ảnh thật qua thấu kính là:

\(L = d + d' = d + \frac{{df}}{{d - f}}\)

\( \Rightarrow {d^2} - Ld + Lf = 0\\ \Rightarrow \Delta  = {L^2} - 4Lf \ge 0 \Rightarrow L \ge 4f\)

\( \Rightarrow {L_{\min }} = 4f\)

Chọn A

Câu 13:

Phương pháp

Sử dụng lý thuyết định nghĩa hiện tượng khúc xạ ánh sáng.

Cách giải

Khúc xạ ánh sáng là hiện tượng lệch phương (gãy) của các tia sáng khi truyền xiên góc qua mặt phân cách giữa hai môi trường trong suốt khác nhau.

Chọn D

Câu 14:

Phương pháp

Sử dụng các công thức \(\left\{ \begin{array}{l}k =  - \frac{{d'}}{d}\\\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\end{array} \right.\)

Cách giải

Ta có: \(k =  - \frac{{d'}}{d} =  - 2 \Leftrightarrow d' = 2{\rm{d}}\)

Lại có: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}} = \frac{1}{d} + \frac{1}{{2{\rm{d}}}} = \frac{1}{{30}} \Rightarrow d = 45cm\)

Chọn A

Câu 15:

Phương pháp

Cách giải

Để quan sát những vật kích thước nhỏ ở khoảng cách gần ta cần dùng kính hiển vi.

Chọn B

Câu 16:

Phương pháp

Sử dụng phương pháp hình học.

Sử dụng công thức lượng giác \({\sin ^2}i + {\cos ^2}i = 1\)

Cách giải

 

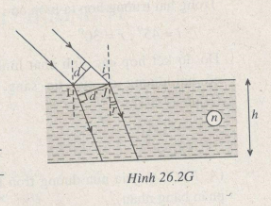
Ta có: d = IJ.cosi; d’ = IJ.cosr

Suy ra: \(d' = \frac{{\cos {\rm{r}}}}{{\cos i}}d\)

Lại có: \(\cos {\rm{r}} = \sqrt {1 - {{\sin }^2}r}  = \sqrt {1 - \frac{{{{\sin }^2}i}}{{{n^2}}}}  = \sqrt {\frac{{{n^2} - {{\sin }^2}i}}{{n\cos i}}} \)

Do đó: \(d' = \frac{{\sqrt {{n^2} - {{\sin }^2}i} }}{{n\cos i}}d = \frac{{\sqrt {1,{5^2} - {{\sin }^2}45} }}{{1,5.\cos 45}}.10 = 12,47mm\)

Chọn D

II. TỰ LUẬN

Câu 1:

Phương pháp

Sử dụng hệ thức lượng trong tam giác.

Sử dụng biểu thức định luật khúc xạ ánh sáng: \({n_1}\sin i = {n_2}\sin r\)

Cách giải

 

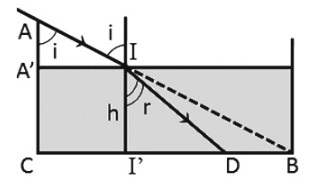
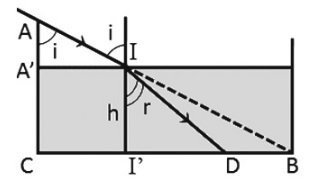
Theo đề bài ta có: AC = 30 cm; CB = 40 cm; A’C = II’ = \(\frac{2}{3}\) AC

Từ hình vẽ ta có:

\(\tan i = \frac{{CI'}}{{AA'}} = \frac{{CB}}{{AC}} = \frac{{40}}{{30}} = \frac{4}{3} \\\Rightarrow i = 53,{1^0} \Rightarrow \sin i = 0,8\)

Theo định luật khúc xạ ánh sáng ta có:

\({n_1}\sin i = {n_2}\sin r\\ \Leftrightarrow \sin r = \frac{{{n_1}\sin i}}{{{n_2}}} = \frac{{1.0,8}}{{\frac{4}{3}}} = 0,6\\ \Rightarrow \tan r = \frac{3}{4}\)

Theo đề bài ta có: \(II' = h = \frac{2}{3}.30 = 20cm\)

\(\tan r = \frac{{I'D}}{{II'}} \Leftrightarrow \frac{3}{4} = \frac{{I'D}}{{20}} \Leftrightarrow I'D = 15cm\)

Mà \(CI' = AA'.\tan i = \left( {AC - II'} \right).tani \\= \left( {30 - 20} \right).\frac{4}{3} = \frac{{40}}{3}cm\)

Suy ra \(d = DB = CB - \left( {CI' + I'D} \right) \\= 40 - \left( {\frac{{40}}{3} + 15} \right) \approx 11,67cm\)

Vậy khoảng cách d cần tìm là \(d \approx 11,67cm\)

Câu 2:

Phương pháp

Sử dụng các công thức: \(\left\{ \begin{array}{l}D = \frac{1}{f}\\k =  - \frac{{d'}}{d}\\\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}}\end{array} \right.\)

Cách giải

a)

Độ tụ của thấu kính \(D = \frac{1}{f} = \frac{1}{{{{20.10}^{ - 2}}}} = 5{\rm{d}}p\)

b)

Ta có: \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}} \Leftrightarrow \frac{1}{{20}} = \frac{1}{{30}} + \frac{1}{{d'}} \Leftrightarrow d' = 60cm\)

Độ phóng đại ảnh \(k = \frac{{ - d'}}{d} = \frac{{ - 60}}{{30}} =  - 2\)

Suy ra: ảnh thật, ngược chiều với vật, có độ lớn gấp hai lần vật, ảnh cách thấu kính một đoạn 60cm.

 

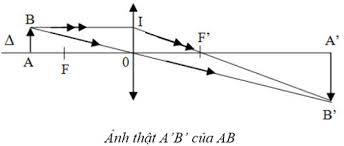
c)

Khoảng cách giữa vật và ảnh là:

Lúc đầu: \({L_1} = {d_1} + d'_1 = 30 + 60 = 90cm\)

Lúc sau: \({L_2} = {L_1} + 8 = 98cm\)

Gọi khoảng cách sau khi dịch chuyển của vật và ảnh lần lượt là \({d_2}\) và\(d'_2\)

\( \Rightarrow {d_2} + d'_2 = 98cm\) (1)

Mà ta có:

\(\frac{1}{f} = \frac{1}{{{d_2}}} + \frac{1}{{d'_2}} \Rightarrow d'_2 = \frac{{{d_2}f}}{{{d_2} - f}}\) (2)

Thay (2) vào (1) ta được:

\({d_2} + \frac{{{d_2}f}}{{{d_2} - f}} = 98 \Leftrightarrow {d_2} + \frac{{20{d_2}}}{{{d_2} - 20}} = 98 \\\Leftrightarrow \left[ \begin{array}{l}{d_2} = 28cm\\{d_2} = 70cm\end{array} \right.\)

Vậy có hai vị trí thu được ảnh rõ nét trên màn đó là ở vị trí cách vật 28 cm hoặc 70 cm. 

+ Với \({d_2} = 28cm \Rightarrow d{'_2} = 98 - 28 = 70cm\) => thấu kính dịch về phía trước một khoảng là \(a = \left| {d{'_1} - d{'_2}} \right| = \left| {60 - 70} \right| = 10cm\)

+ Với \({d_2} = 70cm \Rightarrow d{'_2} = 98 - 70 = 28cm\) => Thấu kính dịch về phía sau một khoảng là \(a = \left| {d{'_1} - d{'_2}} \right| = \left| {60 - 28} \right| = 32cm\)