Giải đề thi học kì 2 lý lớp 10 năm 2019 - 2020 trường THPT Bình Hưng Hòa

Đề bài

Câu 1 (2 điểm): Cho các dữ kiện sau:

- Áp suất tỉ lệ thuật với nhiệt độ tuyệt đối \(\frac{{{V_1}}}{{{T_1}}} = \frac{{{V_2}}}{{{T_2}}}\)

- Nhiệt không thể tự tuyền từ một vật sang vật nóng hơn

- Độ biến thiên nội năng của một vật

- Trong quá trình đẳng tích của một lượng khí nhất định

- Trong quá trình đẳng nhiệt của một lượng khí nhất định

- Áp suất tỉ lệ nghịch với thể tích \({p_1}{V_1} = {p_2}{V_2}\)

- Thể tích tỉ lệ thuận với nhiệt độ tuyệt đối

- Bằng tổng công và nhiệt lượng mà vật nhận được: \(\Delta U = A + Q\)

Dựa vào dữ kiện trên, em hãy ghép lại và viết thành câu hoàn chỉnh:

a) Phát biểu và viết biểu thức Định luật Bôilơ Mảiốt.

b) Phát biểu và viết biểu thức của Nguyên lý I nhiệt động lực học.

Câu 2 (2 điểm): Từ mặt đất, ném một vật lên cao theo phương thẳng đứng với vận tốc 20 m/s. Bỏ qua sức cản không khí. Lấy g = 10 m/s².

a) Tìm độ cao cực đại của vật.

b) Tìm vị trí của vật khi vận tốc có độ lớn 10 m/s.

Câu 3 (1 điểm): Một bình bằng thép dung tích 62 lít chứa khí hidro ở áp suất 4,5 MPa và nhiệt độ 27⁰C. Dùng bình này bơm được bao nhiêu quả bóng bay, biết dung tích mỗi quả 8,5 lít, áp suất 1,05.10⁵ Pa và nhiệt độ trong bóng bay là 13⁰C.

Câu 4 (3 điểm): Một lượng khí Ôxi ở điều kiện tiêu chuẩn (nhiệt độ 0⁰C, áp suất 1 atm) có thể tích 5 lít biến đổi trạng thái qua các quá trình sau:

- Từ trạng thái (1) đến trạng thái (2): đẳng tích, áp suất tăng đến 2 atm.

- Từ trạng thái (2) đến trạng thái (3): đẳng nhiệt, thể tích tăng đến 10 lít. 

a) Tìm các thông số trạng thái ở mỗi trạng thái.

b) Vẽ đồ thị biểu diễn quá trình biến đổi trạng thái của lượng khí trên hệ trục tọa độ (p,V).

Câu 5 (1 điểm): Tại sao về mùa hè ta không nên để xe ngoài trời nắng?

Câu 6 (1 điểm): Một nồi áp suất, bên trong là không khí ở 25⁰C có áp suất bằng áp suất của không khí bên ngoài (1atm). Van bảo hiểm của nồi sẽ mở khi áp suất bên trong cao hơn áp suất bên ngoài 1,2 atm. Nếu nồi được đun nóng tới 180⁰C thì không khí trong nồi đã thoát ra chưa? Áp suất không khí trong nồi bằng bao nhiêu? 

Lời giải chi tiết

HƯỚNG DẪN GIẢI CHI TIẾT

THỰC HIỆN: BAN CHUYÊN MÔN LOIGIAIHAY.COM

Câu 1:

Phương pháp

Sử dụng lý thuyết về quá trình đẳng nhiệt - Định luật Bôilơ Mariốt.

Sử dụng lý thuyết về nguyên lý I nhiệt động lực học.

Cách giải

a) Định luật Bôilơ Mariốt:

Trong quá trình đẳng nhiệt của một lượng khí nhất định, áp suất tỉ lệ nghịch với thể tích \({p_1}{V_1} = {p_2}{V_2}\)

b) Nguyên lý I nhiệt động lực học:

Độ biến thiên nội năng của một vật bằng tổng công và nhiệt lượng mà vật nhận được: \(\Delta U = A + Q\)

Câu 2:

Phương pháp

Sử dụng công thức độc lập với thời gian: \({v^2} - v_0^2 = 2g.h\)

Phương trình độ cao của vật: \(y = {y_0} + {v_0}t + \frac{1}{2}g{t^2}\)

Cách giải

Chọn gốc tọa độ tại mặt đất, chiều dương hướng lên trên. Gốc thời gian là lúc bắt đầu ném vật.

a)

Cách 1:

Phương trình độ cao của vật là

\(y = {y_0} + {v_0}t + \frac{1}{2}g{t^2} \\= 0 + 20t - \frac{1}{2}.10{t^2} = 20t - 5{t^2}\) (1)

Phương trình vận tốc: \(v = {v_0} + gt = 20 - 10t\) (2)

Tại điểm cao nhất \(v = 0\) thay vào (2) suy ra t = 2 s

Thay t = 2s vào (1) ta được \({y_{\max }} = 20.2 - {5.2^2} = 20(m)\)

Cách 2:

Áp dụng công thức độc lập với thời gian \({v^2} - v_0^2 = 2g.h\)

Vật đạt độ cao cực đại tại thời điểm \(v = 0\) \( \Rightarrow {0^2} - {20^2} = 2.( - 10).{h_{\max }} \Rightarrow {h_{\max }} = 20m\)

b)

Áp dụng công thức độc lập với thời gian \({v^2} - v_0^2 = 2g.h\)

\(v = 10 \Rightarrow {10^2} - {20^2} = 2.\left( { - 10} \right).h \\\Leftrightarrow h = 15m\)

Kết luận:

a) Độ cao cực đại là 20 m

b) Khi vật có vận tốc 10 m/s thì vật ở vị trí cách mặt đất 15 m

Câu 3:

Phương pháp

Sử dụng phương trình trạng thái khí lý tưởng: \(\frac{{{p_1}{V_1}}}{{{T_1}}} = \frac{{{p_2}{V_2}}}{{{T_2}}}\)

Cách giải

Trạng thái 1: \({V_1} = 62l;{T_1} = 27 + 273 = 300K;\\{p_1} = 4,5MPa = {45.10^5}Pa\)

Trạng thái 2: \({V_2} = 8,5n + 62;{T_2} = 13 + 273 = 286K;\\{p_2} = 1,{05.10^5}Pa\)

(n là số bóng bơm được)

Phương trình trạng thái:

\(\frac{{{p_1}{V_1}}}{{{T_1}}} = \frac{{{p_2}{V_2}}}{{{T_2}}} \Leftrightarrow \frac{{{{45.10}^5}.62}}{{300}} = \frac{{1,{{05.10}^5}.\left( {8,5n + 62} \right)}}{{286}}\)

\( \Rightarrow n = 291\)

Vậy số bóng bơm được là 291 quả.

Câu 4:

Phương pháp

Áp dụng định luật Saclơ

Áp dụng định luật Bôilơ Mariốt.

Cách giải

Trạng thái 1: \({p_1} = 1{\rm{a}}tm;{T_1} = 0 + 273 = 273K;{V_1} = 5l\)

Trạng thái 2: \({p_2} = 2{\rm{a}}tm;{T_2};{V_2} = {V_1} = 5l\)

Trạng thái 3: \({p_3};{V_3} = 10l;{T_3} = {T_2}\)

a)

Từ trạng thái (1) sang trạng thái (2) là quá trình đẳng tích. Áp dụng định luật Saclơ ta có:

\(\frac{{{p_1}}}{{{T_1}}} = \frac{{{p_2}}}{{{T_2}}} \Rightarrow \frac{1}{{273}} = \frac{2}{{{T_2}}} \Leftrightarrow {T_2} = \frac{{2.273}}{1} = 546K\)

Từ trạng thái (2) đến trạng thái (3) là quá trình đẳng nhiệt. Áp dụng định luật Bôilơ Mariốt ta có:

\({p_2}{V_2} = {p_3}{V_3} \Rightarrow 2.5 = {p_3}.10 \Leftrightarrow {p_3} = \frac{{2.5}}{{10}} = 1{\rm{a}}tm\)

Vậy các thông số ở mỗi trạng thái là:

Trạng thái 1: \({p_1} = 1{\rm{a}}tm;{T_1} = 273K;{V_1} = 5l\)

Trạng thái 2: \({p_2} = 2{\rm{a}}tm;{T_2} = 546K;{V_2} = 5l\)

Trạng thái 3: \({p_3} = 1atm;{V_3} = 10l;{T_3} = 546K\) 

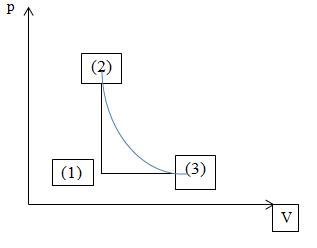
b)

Câu 5:

Phương pháp

Sử dụng lý thuyết sự nở vì nhiệt của chất khí : chất khí nở ra khi nóng lên và co lại khi lạnh đi.

Cách giải

Vì vào mùa hè nhiệt độ thời tiết rất cao, nếu ta để xe ngoài trời nắng thì chất khí trong bánh xe nóng lên, nở ra. Săm xe cản trở sự nở vì nhiệt của không khí gây ra lực lớn làm nổ bánh xe, gây nguy hiểm cho mình và những người xung quanh.

Câu 6:

Phương pháp

Áp dụng biểu thức tính nhiệt độ tuyệt đối \(T = t + 273\)

Vận dụng biểu thức định luật Saclơ \(\frac{p}{T} = const\)

Cách giải

Lượng không khí trong nồi được đun nóng trong một quá trình đẳng tích.

Trạng thái 1: \({T_1} = 25 + 273 = 298K;{p_1} = 1atm\)

Trạng thái 2: \({T_2} = 180 + 273 = 453K;{p_2} = ?\)

Áp dụng biểu thức định luật Saclơ với hai trạng thái (1) và (2) ta được:

\(\frac{{{p_1}}}{{{T_1}}} = \frac{{{p_2}}}{{{T_2}}} \Rightarrow {p_2} = \frac{{{p_1}{T_2}}}{{{T_1}}} = \frac{{1.453}}{{298}} = 1,52atm\) > 1,2atm

Vậy van bảo hiểm đã mở, không khí trong nồi đã được thoát ra.