Đề kiểm tra 45 phút chương 3 phần Hình học 8 - Đề số 2

Đề bài

Câu 1. (3 điểm) Hãy chọn kết quả đúng. Tam giác \(ABC\) có đường phân giác \(AD\left( {D \in BC} \right)\). Cho biết độ dài \(AB = 4,5cm,BD = 2,5cm,\) \(CD = 4cm\). (h.59)

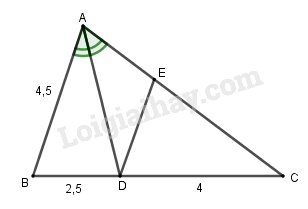
a) Độ dài của cạnh \(AC\) là:

A. \(7,5\)

B. \(7,2\)

C. \(11,7\)

D. \(2,8\)

b) Từ \(D\) kẻ \(DE//AB\left( {E \in AC} \right)\). Độ dài của đoạn thẳng \(DE\) là:

A. \(\dfrac{{36}}{{13}}\)

B. \(\dfrac{{36}}{5}\)

C. \(\dfrac{{36}}{{15}}\)

D. \(\dfrac{9}{5}\)

c) Độ dài của đoạn thẳng \(AE\) là:

A. \(\dfrac{{36}}{5}\)

B. \(\dfrac{{36}}{{13}}\)

C. \(\dfrac{{36}}{{25}}\)

D. \(\dfrac{{36}}{{15}}\)

Câu 2. (7 điểm) Tứ giác \(ABCD\) có hai đường chéo \(AC\) và \(BD\) cắt nhau tại \(O\), \(\widehat {ABD} = \widehat {ACD}\). Gọi \(E\) là giao điểm của hai đường thẳng \(AD\) và \(BC\) (h.60).

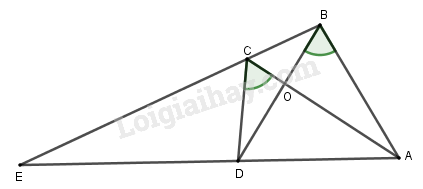
Chứng minh rằng:

a) \(\Delta AOB \backsim \Delta DOC\)

b) \(\Delta AOD \backsim \Delta BOC\)

c) \(EA.ED = EB.EC\)

LG câu 1

Phương pháp:

a) Sử dụng tính chất đường phân giác của tam giác.

b) Sử dụng hệ quả của định lí Ta – let.

c) Sử dụng hệ quả của định lí Ta – let và các kết quả tính được ở trên.

Cách giải:

a) \(AD\) là phân giác của \(\widehat A\) nên \(\dfrac{{BD}}{{DC}} = \dfrac{{AB}}{{AC}}\left( {tc} \right)\) \( \Rightarrow AC = \dfrac{{DC.AB}}{{BD}}\)\( = \dfrac{{4.4,5}}{{2,5}} = \dfrac{{36}}{5} = 7,2\).

Chọn B.

b) \(DE//AB\) nên theo hệ quả của định lý Ta – let ta có:

\(\dfrac{{DE}}{{AB}} = \dfrac{{DC}}{{BC}}\) \( \Rightarrow DE = \dfrac{{AB.DC}}{{BC}} = \dfrac{{4,5.4}}{{4 + 2,5}} = \dfrac{{36}}{{13}}\).

Chọn A.

c) \(ED//AB\) nên theo hệ quả của định lý Ta – let ta có:

\(\dfrac{{AE}}{{AC}} = \dfrac{{BD}}{{BC}}\) \( \Rightarrow AE = \dfrac{{AC.BD}}{{BC}}\) \( = \dfrac{{7,2.2,5}}{{2,5 + 4}} = \dfrac{{36}}{{13}}\)

Chọn B.

LG câu 2

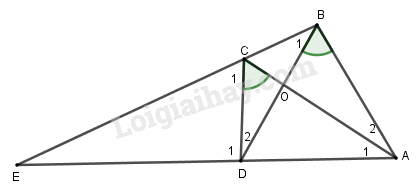
Phương pháp:

a) Sử dụng trường hợp đồng dạng góc – góc.

b) Sử dụng trường hợp đồng dạng cạnh – góc – cạnh.

c) Chứng minh hai tam giác \(ECD\) đồng dạng tam giác \(EAB\) và kết luận.

Cách giải:

a) Xét \(\Delta AOB\) và \(\Delta DOC\) có:

\(\widehat {ABO} = \widehat {DCO}\left( {gt} \right)\)

\(\widehat {AOB} = \widehat {DOC}\) (đối đỉnh)

\( \Rightarrow \Delta AOB \backsim \Delta DOC\) (đpcm).

b) Từ câu a, \(\Delta AOB \backsim \Delta DOC\)\( \Rightarrow \dfrac{{OA}}{{OD}} = \dfrac{{OB}}{{OC}}\left( {c.t.u} \right)\)

xét \(\Delta AOD\) và \(\Delta BOC\) có:

\(\widehat {AOD} = \widehat {BOC}\) (đối đỉnh)

\(\dfrac{{OA}}{{OD}} = \dfrac{{OB}}{{OC}}\left( {cmt} \right)\)

\( \Rightarrow \Delta AOD \backsim \Delta BOC\) (đpcm).

c) Ta có:

\(\widehat {{C_1}}\) là góc ngoài của tam giác \(BCD\) nên \(\widehat {{C_1}} = \widehat {{B_1}} + \widehat {{D_2}}\) (tính chất) (1)

Theo câu a) \(\Delta AOB \backsim \Delta DOC \Rightarrow \widehat {{A_2}} = \widehat {{D_2}}\) (góc tương ứng) (2)

Theo câu b) \(\Delta AOD \backsim \Delta BOC \Rightarrow \widehat {{A_1}} = \widehat {{B_1}}\) (góc tương ứng) (3)

Từ (1), (2) và (3) suy ra \(\widehat {{C_1}} = \widehat {{A_1}} + \widehat {{A_2}} = \widehat {BAE}\)

Xét tam giác \(ECD\) và tam giác \(EAB\) có:

\(\widehat E\) chung

\(\widehat {ECD} = \widehat {EAB}\left( {cmt} \right)\)

\( \Rightarrow \Delta ECD \backsim \Delta EAB\left( {g.g} \right)\)

\( \Rightarrow \dfrac{{EC}}{{EA}} = \dfrac{{ED}}{{EB}}\left( {c.t.u} \right)\) \( \Rightarrow EC.EB = EA.ED\left( {dpcm} \right)\).