Đề kiểm tra 45 phút chương 3 phần Đại số 8 - Đề số 1

Đề bài

Câu 1. (0,5 điểm). Mỗi khẳng định sau đây đúng hay sai?

a) Phương trình \({x^2} + 1 = 0\) vô nghiệm.

b) Phương trình \(x + \dfrac{1}{x} = \dfrac{1}{x}\) có nghiệm.

Câu 2. (0,5 điểm). Cho phương trình (1) có tập nghiệm là \(S_1=\{-4;3\}\). Gọi \(S_2\) là tập nghiệm của phương trình (2). Nếu (2) tương đương với (1) thì:

\(\begin{array}{l}
(A)\,4 \in {S_2}\\
(B)\,3 \in {S_2}\\
(C)\, - 3 \in {S_2}\\
(D)\, - 2 \in {S_2}
\end{array}\)

Hãy chọn khẳng định đúng.

Câu 3. (0,5 điểm). Số \(\dfrac{1}{2}\) là nghiệm của phương trình

\(\begin{array}{l}
(A)\,4 - 2x = 0\\
(B)\,2x + 1 = 0\\
(C)\,6x + 5 = 2\\
(D)\,5 = 6x + 2
\end{array}\)

Hãy chọn khẳng định đúng.

Câu 4. (0,5 điểm). Điều kiện xác định của phương trình \(\dfrac{{2x - 5}}{{2 - 5x}} + 1 = \dfrac{{x - 1}}{{x + 1}}\) là

(A) \(x\ne -1\)

(B) \(x \ne \dfrac{2}{5}\)

(C) \(x\ne -1\) và \(x \ne \dfrac{5}{2}\)

(D) \(x\ne -1\) và \(x \ne \dfrac{2}{5}\)

Hãy chọn khẳng định đúng.

Câu 5. (0,5 điểm). Tập nghiệm của phương trình \(x\left( {x + 15} \right) = 5\left( {x + 15} \right)\) là

(A) \(S=\{5;-15\}\)

(B) \(S=\{5;15\}\)

(C) \(S=\{-5;-15\}\)

(D) \(S=\{-5;15\}\)

Hãy chọn khẳng định đúng.

Câu 6. (0,5 điểm). Tập nghiệm của phương trình \(x\left( {1 - \dfrac{1}{{x - 1}}} \right) = 1 - \dfrac{1}{{x - 1}}\) là

(A) \(S=\{1;2\}\)

(B) \(S=\{-1;2\}\)

(C) \(S=\{2\}\)

(D) \(S=\{1\}\)

Hãy chọn khẳng định đúng.

Câu 7. (4 điểm) Cho hai biểu thức: \(A = \dfrac{{x + 2}}{{y - 1}}\) và \(B = \dfrac{{4x\left( {x + 5} \right)}}{{y + 2}}\)

a) Giả sử đã biết \(y=2\), hãy giải phương trình (ẩn \(x\)): \(A+3=B\).

b) Giả sử đã biết \(x=-3\), háy giải phương trình (ẩn \(y\)): \(A-B=13\).

Câu 8. (3 điểm). Tìm một số tự nhiên có ba chữ số, biết rằng chữ số hàng đơn vị của nó bằng \(5\) và nếu bỏ đi chữ số hàng đơn vị ấy đi thì ta được một số (có hai chữ số) nhỏ hơn số ban đầu \(167\) đơn vị.

Lời giải chi tiết

Câu 1:

Phương pháp:

Giải các phương trình đã cho rồi xét tính đúng sai của mỗi khẳng định.

a) Chú ý: \({x^2} \ge 0\) với mọi \(x\).

b) Tìm ĐKXĐ, giải phương trình.

Lời giải:

a) \({x^2} \ge 0\) với mọi \(x\) do đó \({x^2} + 1 > 0\) với mọi \(x\).

Vậy phương trình \({x^2} + 1 = 0\) vô nghiệm.

Khẳng định a đúng.

b) ĐKXĐ: \(x\ne0\)

\(\begin{array}{l}
x + \dfrac{1}{x} = \dfrac{1}{x}\\
\Leftrightarrow x + \dfrac{1}{x} - \dfrac{1}{x} = 0\\
\Rightarrow x = 0\,\text{(loại)}
\end{array}\)

Vậy phương trình \(x + \dfrac{1}{x} = \dfrac{1}{x}\) vô nghiệm.

Khẳng định b sai.

Câu 2:

Phương pháp:

Sử dụng: Hai phương trình tương đương nếu chúng có cùng tập nghiệm.

Lời giải:

Phương trình (1) và (2) tương đương nên tập nghiệm \(S_1=S_2=\{-4;3\}\).

Chọn B.

Câu 3: 

Phương pháp:

Thay \(x = \dfrac{1}{2}\) vào các phương trình cho ta một khẳng định đúng thì nó là nghiệm của phương trình đó.

Lời giải:

- Thay \(x = \dfrac{1}{2}\) vào phương trình \(4-2x=0\) ta được:

\(4 - 2.\dfrac{1}{2} =3\ne 0\)

Vậy \(x = \dfrac{1}{2}\) không là nghiệm của phương trình \(4-2x=0\).

- Thay \(x = \dfrac{1}{2}\) vào phương trình \(2x+1=0\) ta được:

\(2.\dfrac{1}{2} + 1 =2\ne 0\)

Vậy \(x = \dfrac{1}{2}\) không là nghiệm của phương trình \(2x+1=0\).

- Thay \(x = \dfrac{1}{2}\) vào phương trình \(6x+5=2\) ta được:

\(6.\dfrac{1}{2} + 5 = 8 \ne 2\)

Vậy \(x = \dfrac{1}{2}\) không là nghiệm của phương trình \(6x+5=2\).

- Thay \(x = \dfrac{1}{2}\) vào phương trình \(5=6x+2\) ta được:

\(5 = 6.\dfrac{1}{2} + 2\)

Vậy \(x = \dfrac{1}{2}\) là nghiệm của phương trình \(5=6x+2\).

Chọn D.

Câu 4: 

Phương pháp:

Sử dụng: Điều kiện xác định của phương trình là điều kiện của các mẫu thức khác \(0\).

Lời giải:

Điều kiện xác định của phương trình \(\dfrac{{2x - 5}}{{2 - 5x}} + 1 = \dfrac{{x - 1}}{{x + 1}}\) là:

\(2 - 5x \ne 0\) và \(x + 1 \ne 0\)

Hay \(x \ne \dfrac{2}{5}\) và \(x \ne - 1\)

Chọn D.

Câu 5: 

Phương pháp:

Đưa phương trình đã cho về dạng phương trình tích:

\(\begin{array}{l}
A\left( x \right)B\left( x \right) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
A\left( x \right) = 0\\
B\left( x \right) = 0
\end{array} \right.
\end{array}\)

Lời giải:

\(\begin{array}{l}
x\left( {x + 15} \right) = 5\left( {x + 15} \right)\\
\Leftrightarrow x\left( {x + 15} \right) - 5\left( {x + 15} \right) = 0\\
\Leftrightarrow \left( {x + 15} \right)\left( {x - 5} \right) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
x + 15 = 0\\
x - 5 = 0
\end{array} \right.\\
\Leftrightarrow \left[ \begin{array}{l}
x = - 15\\
x = 5
\end{array} \right.
\end{array}\)

Chọn A.

Câu 6: 

Phương pháp:

Tìm ĐKXĐ của phương trình. Đưa phương trình đã cho về dạng phương trình tích:

\(\begin{array}{l}
A\left( x \right)B\left( x \right) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
A\left( x \right) = 0\\
B\left( x \right) = 0
\end{array} \right.
\end{array}\)

Lời giải:

ĐKXĐ: \(x\ne1\).

\(\begin{array}{l}
x\left( {1 - \dfrac{1}{{x - 1}}} \right) = 1 - \dfrac{1}{{x - 1}}\\
\Leftrightarrow x\left( {1 - \dfrac{1}{{x - 1}}} \right) - \left( {1 - \dfrac{1}{{x - 1}}} \right) = 0\\
\Leftrightarrow \left( {1 - \dfrac{1}{{x - 1}}} \right)\left( {x - 1} \right) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
1 - \dfrac{1}{{x - 1}} = 0\,\,\,\\
x - 1 = 0\,\,\,\,\,\,\,\,
\end{array} \right.\\
\Leftrightarrow \left[ \begin{array}{l}
1 - \dfrac{1}{{x - 1}} = 0\,\,\,(*)\\
x = 1\;\text{(loại)}
\end{array} \right.
\end{array}\)

\(\begin{array}{l}
(*) \Leftrightarrow \dfrac{{x - 1 - 1}}{{x - 1}} = 0\,\\
\Leftrightarrow \dfrac{{x - 2}}{{x - 1}} = 0\\
\Rightarrow x - 2 = 0\\
\Leftrightarrow x = 2\,\,\text{(thỏa mãn ĐKXĐ)}
\end{array}\)

Vậy tập nghiệm của phương trình là \(S=\{2\}\).

Chọn C.

Phương pháp:

a) Thay \(y=2\) vào biểu thức A, B để tính giá trị của biểu thức A, B. Từ đó giải phương trình \(A + 3 = B\).

b) Thay \(x=-3\) vào biểu thức A, B để tính giá trị của biểu thức A, B. Từ đó giải phương trình \(A - B = 13\).

Lời giải:

a) Với \(y=2\) ta có:

\(\begin{array}{l}
A = \dfrac{{x + 2}}{{2 - 1}} = x + 2\\
B = \dfrac{{4x\left( {x + 5} \right)}}{{2 + 2}} = x\left( {x + 5} \right)
\end{array}\)

Khi đó ta có:

\(\begin{array}{l}
A + 3 = B\\
\Leftrightarrow x + 2 + 3 = x\left( {x + 5} \right)\\
\Leftrightarrow x + 5 - x\left( {x + 5} \right) = 0\\
\Leftrightarrow \left( {x + 5} \right)\left( {1 - x} \right) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
x + 5 = 0\\
1 - x = 0
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
x = - 5\\
x = 1
\end{array} \right.
\end{array}\)

b) Với \(x=-3\) ta có:

\(\begin{array}{l}
A = \dfrac{{ - 3 + 2}}{{y - 1}} = \dfrac{{ - 1}}{{y - 1}}\\
B = \dfrac{{4.\left( { - 3} \right).\left( { - 3 + 5} \right)}}{{y + 2}} = \dfrac{{ - 24}}{{y + 2}}
\end{array}\)

Khi đó ta có:

\(\begin{array}{l}
A - B = 13\\
\Leftrightarrow \dfrac{{ - 1}}{{y - 1}} - \dfrac{{ - 24}}{{y + 2}} = 13
\end{array}\)

ĐKXĐ: \(y\ne1;y\ne -2\).

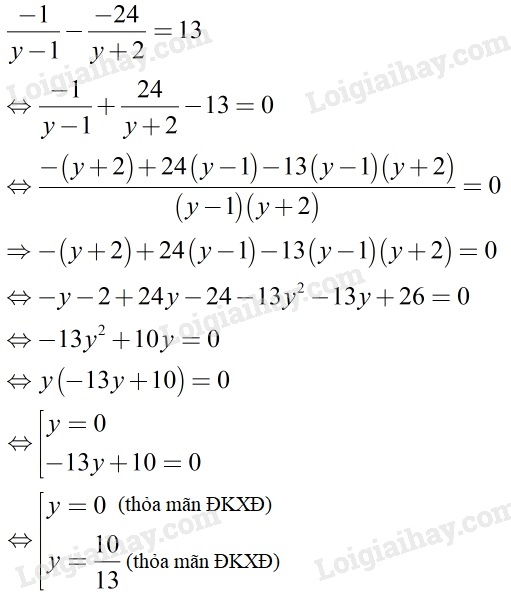
Câu 8:

Phương pháp:

Các bước giải bài toán bằng cách lập phương trình:

Bước 1: Lập phương trình

- Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số.

- Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết.

- Lập phương trình biểu thị mối quan hệ giữa các đại lượng.

Bước 2. Giải phương trình

Bước 3: Trả lời

Kiểm tra xem trong các nghiệm của phương trình, nghiệm nào thoả mãn điều kiện của ẩn, nghiệm nào không, rồi kết luận.

Lời giải:

Gọi số cần tìm có dạng \(\overline {x5} \) (\(x\) là số có hai chữ số).

Nếu bỏ đi chữ số hàng đơn vị ấy đi thì ta được một số (có hai chữ số) nhỏ hơn số ban đầu \(167\) đơn vị nên ta có:

\(\begin{array}{l}
\overline {x5} = x + 167\\
\Leftrightarrow x.10 + 5 = x + 167\\
\Leftrightarrow 10x - x = 167 - 5\\
\Leftrightarrow 9x = 162\\
\Leftrightarrow x = 162:9 = 18\text{ (thỏa mãn)}
\end{array}\)

Vậy số cần tìm là \(185\).