Giải câu 5, 6, 7, 8, vui học trang 42, 43

Giải Cùng em học Toán lớp 5 tập 2 tuần 28 câu 5, 6, 7, 8, vui học trang 42, 43 với lời giải chi tiết. Câu 5. Điền dấu (>,<,=) thích hợp vào chỗ chấm : 345 687 ... 345 678 ; ...

Bài 5

Điền dấu (>,<,=) thích hợp vào chỗ chấm:

\(345\,687 \ldots 345\,678\)

\(9999 \ldots 10\,001\)

\(798 \ldots 801\)

\(\dfrac{8}{{15}} \ldots \dfrac{7}{{15}}\)

\(\dfrac{{14}}{{15}} \ldots \dfrac{7}{{15}}\)

\(\dfrac{{15}}{{32}} \ldots \dfrac{{45}}{{96}}\)

Phương pháp giải:

* Áp dụng quy tắc so sánh hai số tự nhiên:

Trong hai số tự nhiên:

- Số nào có nhiều chữ số hơn thì số kia lớn hơn. Số nào có ít chữ số hơn thì bé hơn.

- Nếu hai số có chữ số bằng nhau thì so sánh từng cặp chữ số ở cùng một hàng kể từ trái sang phải.

* Áp dụng quy tắc so sánh hai phân số có cùng mẫu số:

Trong hai phân số có cùng mẫu số:

- Phân số nào có tử số bé hơn thì phân số đó bé hơn.

- Phân số nào có tử số lớn hơn thì phân số đó lớn hơn.

- Nếu tử số bằng nhau thì hai phân số đó bằng nhau.

* Áp dụng quy tắc so sánh hai phân số khác mẫu số:

Muốn so sánh hai phân số khác mẫu số, ta có thể quy đồng mẫu số hai phân số đó rồi so sánh các tử số của hai phân số mới.

Lời giải chi tiết:

\(345\,687 > 345\,678\)

\(9999 < 10\,001\)

\(798 < 801\)

\(\dfrac{8}{{15}} > \dfrac{7}{{15}}\)

\(\dfrac{{14}}{{15}} > \dfrac{7}{{15}}\)

\(\dfrac{{15}}{{32}} = \dfrac{{15 \times 3}}{{32 \times 3}} = \dfrac{{45}}{{96}}\)

Bài 6

Viết chữ số thích hợp vào ô trống để được số:

a) 35 ☐ chia hết cho cả 2 và 5.

b) 67 ☐ chia hết cho cả 2 và 3

c) 76 ☐ chia hết cho cả 9 và 5.

d) 7 ☐ 5 chia hết cho 3 và 5 .

Phương pháp giải:

Áp dụng các dấu hiệu chia hết cho 2; 3; 5; 9:

- Các số có chữ số tận cùng là 0; 2; 4; 6; 8 thì chia hết cho 2.

- Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5.

- Các số có tổng các chữ số chia hết cho 9 thì chia hết cho 9.

- Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 3.

- Các số có chữ số tận cùng là 0 thì chia hết cho cả 2 và 5.

Lời giải chi tiết:

a) Để số 35 ☐ chia hết cho cả 2 và 5 thì chữ số điền vào ô trống là 0.

b) Để số 67 ☐ chia hết cho 3 thì tổng các chữ số phải chia hết cho 3, hay 6 + 7 + ☐ chia hết cho 3, hay 13 + ☐ chia hết cho 3.

Suy ra chữ số điền vào ô trống có thể là 2; 5; 8.

Mà các số có chữ số tận cùng là 0; 2; 4; 6; 8 thì chia hết cho 2.

Vậy để số 67 ☐ chia hết cho cả 2 và 3 thì chữ số thích hợp điền vào ô trống là 2 hoặc 8.

c) Để số 76 ☐ chia hết cho 5 thì chữ số cần điền vào ô trống có thể là 0 hoặc 5.

Số 760 có tổng các chữ số là \(7 + 6 + 0 = 13\). Mà 13 không chia hết cho 9 nên số 760 không chia hết cho 9.

Số 765 có tổng các chữ số là \(7 + 6 + 5 = 18\). Mà 18 chia hết cho 9 nên số 765 chia hết cho 9.

Vậy để số 76 ☐ chia hết cho cả 9 và 5 thì chữ số cần điền vào ô trống là 5.

d) Để số 7 ☐ 5 chia hết cho 3 thì tổng các chữ số phải chia hết cho 3, hay 7 + ☐ + 5 chia hết cho 3, hay 12 + ☐ chia hết cho 3.

Suy ra chữ số điền vào ô trống có thể là 0; 3; 6; 9.

Số 7 ☐ 5 có chữ số tận cùng là 5 nên luôn chia hết cho 5.

Vậy để số 7 ☐ 5 chia hết cho 3 và 5 thì chữ số cần điền vào ô trống có thể là 0; 3; 6; 9.

Bài 7

Quy đồng mẫu số các phân số:

\(\dfrac{2}{3}\) và \(\dfrac{3}{4}\) ; \(\dfrac{1}{3};\dfrac{3}{5}\) và \(\dfrac{5}{6}\)

Phương pháp giải:

Khi quy đồng mẫu số hai phân số có thể làm như sau:

- Lấy tử số và mẫu số của phân số thứ nhất nhân với mẫu số của phân số thứ hai.

- Lấy tử số và mẫu số của phân số thứ hai nhân với mẫu số của phân số thứ nhất.

Lời giải chi tiết:

a) Chọn mẫu số chung là 20.

Quy đồng mẫu số hai phân số \(\dfrac{2}{5}\) và \(\dfrac{3}{4}\) ta có:

\(\dfrac{2}{5} = \dfrac{{2 \times 4}}{{5 \times 4}} = \dfrac{8}{{20}};\)

\(\dfrac{3}{4} = \dfrac{{3 \times 5}}{{4 \times 5}} = \dfrac{{15}}{{20}}.\)

b) Chọn mẫu số chung là 30.

Quy đồng mẫu số hai phân số \(\dfrac{1}{3};\,\,\dfrac{3}{5}\) và \(\dfrac{5}{6}\) ta có:

\(\dfrac{1}{3} = \dfrac{{1 \times 10}}{{3 \times 10}} = \dfrac{{10}}{{30}};\)

\(\dfrac{3}{5} = \dfrac{{3 \times 6}}{{5 \times 6}} = \dfrac{{18}}{{30}};\)

\(\dfrac{5}{6} = \dfrac{{5 \times 5}}{{6 \times 5}} = \dfrac{{25}}{{30}}\).

Bài 8

Ba điểm A, B, C lần lượt cùng nằm trên một tuyến đường. Một ô tô xanh đi từ B đến C với vận tốc 48km/giờ, cùng lúc đó một ô tô đen đi từ A theo hướng qua B tới C với vận tốc 64km/giờ và đuổi theo ô tô xanh (xem hình dưới đây). Hỏi sau bao lâu ô tô đen đuổi kịp ô tô xanh, biết khoảng cách từ A đến B là 32km?

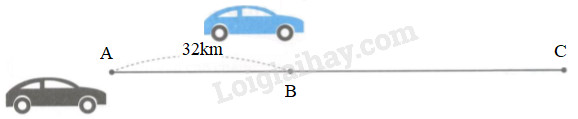
Phương pháp giải:

Theo đề bài, hai ô tô xuất phát cùng lúc và chuyển động cùng chiều với nhau. Để giải bài này ta làm như sau:

- Tính số ki-lô-mét mỗi giờ ô tô đen gần ô tô xanh.

- Thời gian đi để ô tô đen đuổi kịp ô tô xanh bằng khoảng cách ban đầu giữa hai xe (tức là độ dài quãng đường AB) chia cho số ki-lô-mét mỗi giờ ô tô đen gần ô tô xanh.

Lời giải chi tiết:

Mỗi giờ ô tô đen gần ô tô xanh số ki-lô-mét là:

\(64 – 48 = 16\;(km)\)

Ô tô đen đuổi kịp ô tô xanh sau số thời gian là:

\(32 : 16 = 2\) (giờ)

Đáp số : \(2\) giờ.

Vui học

Buổi sáng, Hùng và Huy cùng chạy tập thể dục xung quanh một bờ hồ có chu vi 1000m (cùng chạy từ một chỗ và cùng một lúc). Nếu hai bạn chạy ngược chiều nhau thì từ lúc xuất phát đến lúc gặp nhau của hai bạn là 3 phút 20 giây, còn nếu chạy cùng chiều nhau thì từ lúc xuất phát đến lúc gặp nhau là 20 phút. Tính vận tốc của mỗi bạn biết Hùng chạy nhanh hơn Huy.

Phương pháp giải:

- Từ công thức tính thời gian đi để hai xe gặp nhau giữa hai xe chuyển động ngược chiều, xuất phát cùng lúc ta suy ra:

Tổng hai vận tốc = Quãng đường : thời gian đi để gặp nhau.

- Từ công thức tính thời gian đi để hai xe gặp nhau giữa hai xe chuyển động cùng chiều, xuất phát cùng lúc ta suy ra:

Hiệu hai vận tốc = Quãng đường : thời gian đi để gặp nhau.

- Áp dụng hai công thức trên ta tìm được tổng và hiệu vận tốc của hai bạn.

- Áp dụng công thức tìm hai số khi biết tổng và hiệu của hai số đó ta tìm được vận tốc của mỗi bạn:

Số lớn = (Tổng + Hiệu) : 2 ;

Số bé = (Tổng – Hiệu) : 2.

Lời giải chi tiết:

Đổi: \(3\) phút \(20\) giây \(= 3\dfrac{1}{3}\) phút \(= \dfrac{{10}}{3}\) phút.

Tổng vận tốc của hai bạn là