Giải câu hỏi trang 68, 69, 70 SGK Toán 9 tập 2 - Kết nối tri thức

HĐ

Trả lời câu hỏi Hoạt động trang 68 SGK Toán 9 Kết nối tri thức

Vẽ đường tròn tâm O có bán kính bằng 2cm và dây cung AB có độ dài bằng 2cm. Lấy một điểm C tùy ý nằm trên cung lớn AmB (H.9.2).

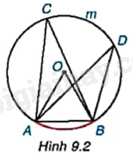
a) Cho biết số đo góc ở tâm AOB và số đo của cung bị chắn AB.

b) Đo góc ACB và so sánh với kết quả của bạn bên cạnh.

c) Lấy điểm D tùy ý nằm trên cung ACB. Đo góc ADB và so sánh với các góc ACB và AOB.

Phương pháp giải:

a) Chứng minh tam giác AOB đều, suy ra \(\widehat {AOB} = {60^o}\). Do đó, \(sđ\overset\frown{AB}=\widehat{AOB}={{60}^{o}}\) (góc ở tâm chắn cung AB).

b, c) Sử dụng thước đo góc đo được góc ACB, góc ADB đều bằng 30 độ. Do đó, \(\widehat {ACB} = \widehat {ADB}\)

Lời giải chi tiết:

Vì A, B thuộc đường tròn tâm O nên \(OA = OB = 2cm\).

Tam giác AOB có: \(OA = OB = AB = 2cm\) nên tam giác ABO đều.

Do đó, \(\widehat {AOB} = {60^o}\).

Suy ra: \(sđ\overset\frown{AB}=\widehat{AOB}={{60}^{o}}\) (góc ở tâm chắn cung AB).

b) Sử dụng thước đo góc, ta đo được \(\widehat {ACB} = {30^o}\).

c) Sử dụng thước đo góc, ta đo được \(\widehat {ADB} = {30^o}\). Do đó, \(\widehat {ACB} = \widehat {ADB}\).

CH

Trả lời câu hỏi Câu hỏi trang 70 SGK Toán 9 Kết nối tri thức

Hãy cho biết số đo góc nội tiếp tìm được trong Hình 9.3 ở Ví dụ 1, biết rằng số đo của các cung màu xanh trong hình đều bằng \({120^o}\).

Phương pháp giải:

Vì B là góc nội tiếp trong đường tròn nên có số đo bằng nửa số đo cung bị chắn, từ đó tính được góc B.

Lời giải chi tiết:

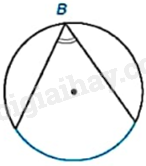
Vì B là góc nội tiếp trong đường tròn nên \(\widehat B = \frac{1}{2}{.120^o} = {60^o}\).

LT

Trả lời câu hỏi Luyện tập trang 70 SGK Toán 9 Kết nối tri thức

Cho đường tròn tâm O và hai dây cung AB, CD cắt nhau tại điểm X nằm trong đường tròn (H.9.6). Chứng minh rằng $\Delta AXC\backsim \Delta DXB$.

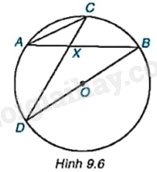
Phương pháp giải:

+ Sử dụng định lí về mối quan hệ giữa góc nội tiếp và cung bị chắn để chứng minh \(\widehat {ACX} = \widehat {XBD}\).

+ Chứng minh $\Delta AXC\backsim \Delta DXB$ theo trường hợp góc – góc.

Lời giải chi tiết:

Vì góc ACX và góc XBD là góc nội tiếp cùng chắn cung AD của đường tròn tâm O nên: \(\widehat {ACX} = \widehat {XBD}\).

Tam giác AXC và tam giác DXB có: \(\widehat {ACX} = \widehat {XBD}\) (cmt), \(\widehat {AXC} = \widehat {BXD}\) (hai góc đối đỉnh).

Do đó, $\Delta AXC\backsim \Delta DXB$ (g – g).

VD

Trả lời câu hỏi Vận dụng trang 70 SGK Toán 9 Kết nối tri thức

Trở lại tình huống mở đầu, hãy tính số đo của góc BAC nếu đường tròn có bán kính 2cm và dây cung \(BC = 2\sqrt 2 cm\).

Chúng ta đã biết số đo góc ở tâm BOC của đường tròn (O) trong Hình 9.1 bằng số đo của cung bị chắn.

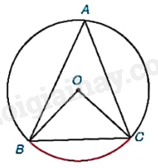
Phương pháp giải:

+ Theo định lí Pythagore đảo chứng minh được tam giác BOC vuông tại O, tính được góc BOC.

+ Vì góc BOC và góc BAC lần lượt là góc ở tâm và góc nội tiếp cùng chắn cung BC của đường tròn (O) nên \(\widehat {BAC} = \frac{1}{2}\widehat {BOC}\).

Lời giải chi tiết:

Vì B, C thuộc đường tròn (O) nên \(OB = OC = 2cm\).

Xét tam giác BOC có: \(O{B^2} + O{C^2} = B{C^2}\left( {do\;{2^2} + {2^2} = {{\left( {2\sqrt 2 } \right)}^2}} \right)\) nên tam giác BOC vuông tại O (định lí Pythagore đảo).

Suy ra, \(\widehat {BOC} = {90^o}\)

Vì góc BOC và góc BAC lần lượt là góc ở tâm và góc nội tiếp cùng chắn cung BC của đường tròn (O) nên \(\widehat {BAC} = \frac{1}{2}\widehat {BOC} = \frac{1}{2}{.90^o} = {45^o}\).