Giải câu hỏi trang 59, 60 SGK Toán 8 - Cùng khám phá
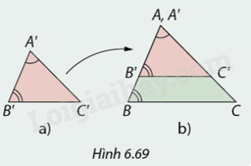
Cắt \(\Delta A'B'C'\) và \(\Delta ABC\) bằng giấy có \(\widehat {A'} = \widehat A\) và \(\widehat {B'} = \widehat B\).
Hoạt động
Cắt \(\Delta A'B'C'\) và \(\Delta ABC\) bằng giấy có \(\widehat {A'} = \widehat A\) và \(\widehat {B'} = \widehat B\). Xếp \(\Delta A'B'C'\) lên \(\Delta ABC\) sao cho cạnh \(A'B'\) chồng lên cạnh \(AB\) và cạnh \(A'C'\) chồng lên cạnh \(AC\) như Hình 6.69.
1. Vì sao trong Hình 6.69b, cạnh \(B'C'\) song song với cạnh \(BC\)
2. Hãy đưa ra kết luận về \(\Delta A'B'C'\) và \(\Delta ABC\).
Phương pháp giải:
Dựa vào tính chất hai đường thẳng song song để chứng minh cạnh \(B'C'\) song song với cạnh \(BC\), sau đó nhận xét về \(\Delta A'B'C'\) và \(\Delta ABC\).
Lời giải chi tiết:
1. Ta có:
\(\widehat {A'B'C'} = \widehat {ABC}\) (gt)
Mà hai góc này ở vị trí so le trong
=> \(B'C'//BC\).
2. Áp dụng định lý học ở bài 4, ta có:
\(\Delta A'B'C'\)∽\(\Delta ABC\).
Luyện tập
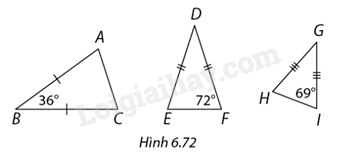
Chỉ ra cặp tam giác đồng dạng trong Hình 6.72.
Phương pháp giải:
Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
Lời giải chi tiết:
Xét tam giác cân \(ABC\), ta có:
\(\widehat A = \widehat C = \frac{{180^\circ - \widehat B}}{2} = \frac{{180^\circ - 36^\circ }}{2} = 72^\circ \)
Xét tam giác cân \(DEF\), ta có:
\(\begin{array}{l}\widehat E = \widehat F = 72^\circ \\\widehat D = 180^\circ - \left( {\widehat E + \widehat F} \right) = 180^\circ - \left( {72^\circ + 72^\circ } \right) = 36^\circ \end{array}\)
Xét tam giác cân \(GHI\), ta có:
\(\begin{array}{l}\widehat H = \widehat I = 69^\circ \\\widehat G = \frac{{180^\circ - \left( {\widehat H + \widehat I} \right)}}{2} = \frac{{180^\circ - \left( {69^\circ + 69^\circ } \right)}}{2} = 21^\circ \end{array}\)
Ta thấy tam giác \(ABC\) và tam giác \(EDF\) có:
\(\begin{array}{l}\widehat A = \widehat F = 72^\circ \\\widehat B = \widehat D = 36^\circ \end{array}\)
=> \(\Delta ABC\)∽\(\Delta EDF\) (g-g)
Vận dụng
Trong Hình 6.73a, đỉnh \(\left( M \right)\), gốc \(\left( N \right)\) của cây dừa và vị trí bạn Phương đứng \(\left( P \right)\) tạo thành tam giác \(MNP\). Phương đo được \(\widehat N = 77^\circ ,\widehat P = 43^\circ \) và \(NP = 20m\). Phương vẽ tam giác \(ABC\) có \(\widehat B = 77^\circ ,\widehat C = 43^\circ \) và \(BC = 10cm\) (Hình 6.73b), đo độ dài cạnh \(AB\) và từ đó tính chiều cao \(MN\) của cây dừa. Em hãy giải thích cách làm của Phương và tính chiều cao \(MN\) của cây dừa nếu \(AB = 7,9cm\)

Phương pháp giải:
Dựa vào trường hợp đồng dạng góc góc: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
Lời giải chi tiết:
Xét tam giác \(MNP\) và tam giác \(ABC\) ta có:
\(\begin{array}{l}\widehat N = \widehat B = 77^\circ \\\widehat P = \widehat C = 43^\circ \end{array}\)
=>\(\Delta MNP\)∽\(\Delta ABC\) (g-g)
Ta có tỉ số đồng dạng:
\(\begin{array}{l}\frac{{MN}}{{AB}} = \frac{{NP}}{{BC}} = \frac{{MP}}{{AC}}\\ \Leftrightarrow \frac{{MN}}{{7,9}} = \frac{{20}}{{10}}\\ \Rightarrow MN = 15,8\end{array}\)
Vậy chiều cao của cây dừa là 15,8 m.
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải câu hỏi trang 59, 60 SGK Toán 8 - Cùng khám phá timdapan.com"







