Giải bài tập 9.41 trang 92 SGK Toán 9 tập 2 - Kết nối tri thức
Cho tam giác ABC nội tiếp đường tròn (O). Gọi M, N, P lần lượt là trung điểm của các cạnh BC, CA, AB. Chứng minh rằng các tứ giác ANOP, BPOM, CMON là các tứ giác nội tiếp.
Đề bài
Cho tam giác ABC nội tiếp đường tròn (O). Gọi M, N, P lần lượt là trung điểm của các cạnh BC, CA, AB. Chứng minh rằng các tứ giác ANOP, BPOM, CMON là các tứ giác nội tiếp.
Phương pháp giải - Xem chi tiết
+ Chứng minh được \(OM \bot BC,ON \bot AC,OP \bot AB\).
+ Chứng minh \(\Delta \)ANO vuông tại N và \(\Delta \)AOP vuông tại P nên tứ giác ANOP là tứ giác nội tiếp.
+ Chứng minh \(\Delta \)CNO vuông tại N và \(\Delta \)COM vuông tại M nên tứ giác CMON là tứ giác nội tiếp.
+ Chứng minh \(\Delta \)MOB vuông tại M và \(\Delta \)BOP vuông tại P nên tứ giác BPOM là tứ giác nội tiếp.
Lời giải chi tiết
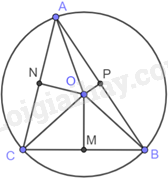
\(\Delta \)AOB có \(OA = OB\) (bán kính đường tròn (O)) nên \(\Delta \)OAB cân tại O, OP là đường trung tuyến đồng thời là đường cao. Suy ra: \(OP \bot AB\) nên \(\Delta \)OPA vuông tại P và \(\Delta \)OBP vuông tại P.
Chứng minh tương tự ta có: \(\Delta \)MOB vuông tại M, \(\Delta \)COM vuông tại M, \(\Delta \)NOC vuông tại N, \(\Delta \)NOA vuông tại N.
Vì \(\Delta \)OPA vuông tại P nên P thuộc đường tròn đường kính AO, \(\Delta \)NOA vuông tại N nên N thuộc đường tròn đường kính AO. Do đó, tứ giác ANOP nội tiếp đường tròn đường kính AO.
Vì \(\Delta \)OPB vuông tại P nên P thuộc đường tròn đường kính BO, \(\Delta \)MOB vuông tại M nên M thuộc đường tròn đường kính BO. Do đó, tứ giác BPOM nội tiếp đường tròn đường kính BO.
Vì \(\Delta \)COM vuông tại M nên M thuộc đường tròn đường kính CO, \(\Delta \)NOC vuông tại N nên N thuộc đường tròn đường kính CO. Do đó, tứ giác CMON nội tiếp đường tròn đường kính CO.
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài tập 9.41 trang 92 SGK Toán 9 tập 2 - Kết nối tri thức timdapan.com"







