Giải bài tập 6.45 trang 30 SGK Toán 9 tập 2 - Kết nối tri thức
Vẽ đồ thị của các hàm số \(y = \frac{5}{2}{x^2}\) và \(y = - \frac{5}{2}{x^2}\) trên cùng một mặt phẳng tọa độ.
Đề bài
Vẽ đồ thị của các hàm số \(y = \frac{5}{2}{x^2}\) và \(y = - \frac{5}{2}{x^2}\) trên cùng một mặt phẳng tọa độ.
Phương pháp giải - Xem chi tiết
Cách vẽ đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\):
+ Lập bảng ghi một số cặp giá trị tương ứng của x và y.
+ Trong mặt phẳng tọa độ Oxy, biểu diễn các cặp điểm (x; y) trong bảng giá trị trên và nối chúng lại để được một đường cong là đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\).
Lời giải chi tiết
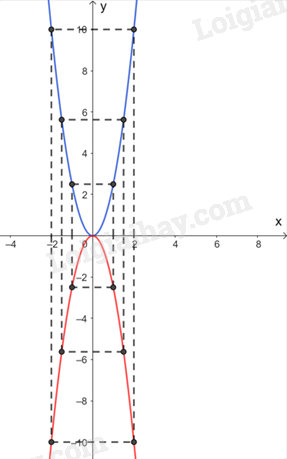
Vẽ đồ thị hàm số \(y = \frac{5}{2}{x^2}\):
Lập bảng một số cặp giá trị tương ứng của x và y:

Biểu diễn các điểm \(\left( { - 2;10} \right);\left( {\frac{{ - 3}}{2};\frac{{45}}{8}} \right);\left( { - 1;\frac{5}{2}} \right);\left( {0;0} \right);\left( {1;\frac{5}{2}} \right),\left( {\frac{3}{2};\frac{{45}}{8}} \right);\left( {2;10} \right)\) trên mặt phẳng tọa độ Oxy và nối chúng lại ta được đồ thị hàm số \(y = \frac{5}{2}{x^2}\) như hình vẽ (đường màu xanh).
Vẽ đồ thị hàm số \(y = - \frac{5}{2}{x^2}\):
Lập bảng một số cặp giá trị tương ứng của x và y:

Biểu diễn các điểm \(\left( { - 2; - 10} \right);\left( {\frac{{ - 3}}{2}; - \frac{{45}}{8}} \right);\left( { - 1; - \frac{5}{2}} \right);\left( {0;0} \right);\left( {1; - \frac{5}{2}} \right),\left( {\frac{3}{2}; - \frac{{45}}{8}} \right);\left( {2; - 10} \right)\) trên mặt phẳng tọa độ Oxy và nối chúng lại ta được đồ thị hàm số \(y = - \frac{5}{2}{x^2}\) như hình vẽ (đường màu đỏ).
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài tập 6.45 trang 30 SGK Toán 9 tập 2 - Kết nối tri thức timdapan.com"







