Giải bài tập 6.14 trang 17 SGK Toán 9 tập 2 - Kết nối tri thức
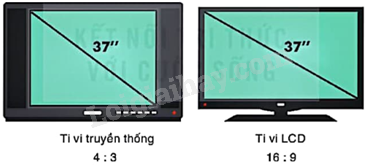
Kích thước màn hình ti vi hình chữ nhật được xác định bằng độ dài đường chéo. Ti vi truyền thống có định dạng 4:3, nghĩa là tỉ lệ giữa chiều dài và chiều rộng của màn hình là 4:3. Hỏi diện tích của màn hình ti vi truyền thống 37in là bao nhiêu? Diện tích của màn hình ti vi LCD 37 in có định dạng 16:9 là bao nhiêu? Màn hình ti vi nào có diện tích lớn hơn? Ở đây, các diện tích màn hình được tính bằng inch vuông.
Đề bài
Kích thước màn hình ti vi hình chữ nhật được xác định bằng độ dài đường chéo. Ti vi truyền thống có định dạng 4:3, nghĩa là tỉ lệ giữa chiều dài và chiều rộng của màn hình là 4:3. Hỏi diện tích của màn hình ti vi truyền thống 37in là bao nhiêu? Diện tích của màn hình ti vi LCD 37 in có định dạng 16:9 là bao nhiêu? Màn hình ti vi nào có diện tích lớn hơn? Ở đây, các diện tích màn hình được tính bằng inch vuông.
Phương pháp giải - Xem chi tiết
+ Gọi chiều dài của ti vi là x, đặt điều kiện, tính chiều rộng theo x.
+ Áp dụng định lý Pythagore để đưa ra phương trình theo ẩn x.
+ Giải phương trình ẩn x, tìm nghiệm x, đối chiếu với điều kiện để tìm giá trị x thỏa mãn điều kiện.
+ Tính diện tích của ti vi.
+ So sánh diện tích của ti vi truyền thống và ti vi LCD và đưa ra kết luận.
Lời giải chi tiết
+) Gọi chiều dài của ti vi truyền thống là x (in, \(x > 0\)) thì chiều rộng của ti vi truyền thống là \(\frac{3}{4}x\left( {in} \right)\)
Khi đó ta có: \({x^2} + {\left( {\frac{3}{4}x} \right)^2} = {37^2}\) (định lý Pythagore)
\(\frac{{25}}{{16}}{x^2} = 1369\)
\(x = \frac{{148}}{5}\) (do \(x > 0\))
Diện tích của ti vi truyền thống là: \(\frac{{148}}{5}.\frac{3}{4}.\frac{{148}}{5} = 675,12\left( {i{n^2}} \right)\)
+) Gọi chiều dài của ti vi LCD là y (in, \(y > 0\)) thì chiều rộng của ti vi LCD là \(\frac{9}{{16}}y\left( {in} \right)\)
Khi đó ta có: \({y^2} + {\left( {\frac{9}{{16}}y} \right)^2} = {37^2}\) (định lý Pythagore)
\(\frac{{337}}{{256}}{y^2} = 1369\)
\({y^2} = \frac{{350464}}{{337}}\)
Diện tích của ti vi LCD là:
\(\frac{9}{{16}}{y^2} = \frac{9}{{16}}.\frac{{350464}}{{337}} = \frac{{197136}}{{337}}\left( {i{n^2}} \right)\)
Vì \(\frac{{197136}}{{337}} < 675,12\) nên màn hình ti vi truyền thống có diện tích lớn hơn.
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài tập 6.14 trang 17 SGK Toán 9 tập 2 - Kết nối tri thức timdapan.com"







