Giải bài tập 10.6 trang 100 SGK Toán 9 tập 2 - Kết nối tri thức
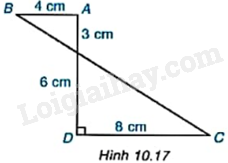
Tính thể tích của hình tạo thành khi cho hình ABCD quanh AD một vòng (H.10.17).
Đề bài
Tính thể tích của hình tạo thành khi cho hình ABCD quanh AD một vòng (H.10.17).
Phương pháp giải - Xem chi tiết
Khi quay hình ABCD quanh cạnh AD một vòng thì ta được một hình gồm hai hình nón có:
+ Hình nón thứ nhất có chiều cao bằng 3cm, bán kính đáy bằng 4cm.
+ Hình nón thứ hai có chiều cao bằng 6cm, bán kính đáy bằng 8cm.
Thể tích của hình nón bán kính r và chiều cao h là: \(V = \frac{1}{3}\pi {r^2}h\).
Lời giải chi tiết
Khi quay hình ABCD quanh cạnh AD một vòng thì ta được một hình gồm hai hình nón có:
+ Hình nón thứ nhất có chiều cao bằng 3cm, bán kính đáy bằng 4cm.
+ Hình nón thứ hai có chiều cao bằng 6cm, bán kính đáy bằng 8cm.
Thể tích hình nón thứ nhất là: \({V_1} = \frac{1}{3}\pi {.4^2}.3 = 16\pi \left( {c{m^3}} \right)\).
Thể tích hình nón thứ hai là: \({V_2} = \frac{1}{3}\pi {.8^2}.6 = 128\pi \left( {c{m^3}} \right)\).
Thể tích hình cần tìm là: \(V = {V_1} + {V_2} = 16\pi + 128\pi = 144\pi \left( {c{m^3}} \right)\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài tập 10.6 trang 100 SGK Toán 9 tập 2 - Kết nối tri thức timdapan.com"







