Giải bài tập 10.27 trang 109 SGK Toán 9 tập 2 - Kết nối tri thức
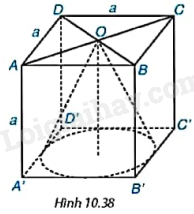
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Tính thể tích của hình nón có đỉnh là tâm O của hình vuông ABCD và đáy là hình tròn tiếp xúc với các cạnh của hình vuông A’B’C’D’ (H.10.38).
Đề bài
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Tính thể tích của hình nón có đỉnh là tâm O của hình vuông ABCD và đáy là hình tròn tiếp xúc với các cạnh của hình vuông A’B’C’D’ (H.10.38).
Phương pháp giải - Xem chi tiết
+ Hình nón có chiều cao \(h = a\), bán kính đáy \(R = \frac{{A'B'}}{2} = \frac{a}{2}\).
+ Thể tích hình nón chiều cao h, bán kính R là: \(V = \frac{1}{3}\pi {R^2}h\).
Lời giải chi tiết
Hình nón đã cho có chiều cao \(h = a\).
Vì đáy hình nón là đường tròn nội tiếp hình vuông A’B’C’D’ nên bán kính đáy là:
\(R = \frac{{A'B'}}{2} = \frac{a}{2}\).
Thể tích của hình nón là:
\(V = \frac{1}{3}\pi {R^2}h = \frac{1}{3}\pi {\left( {\frac{a}{2}} \right)^2}a = \frac{{{a^3}\pi }}{{12}}\).
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài tập 10.27 trang 109 SGK Toán 9 tập 2 - Kết nối tri thức timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài tập 10.27 trang 109 SGK Toán 9 tập 2 - Kết nối tri thức timdapan.com"







