Giải bài 9.4 trang 82 SGK Toán 8 tập 2 - Kết nối tri thức
Cho tam giác ABC cân tại đỉnh A
Đề bài
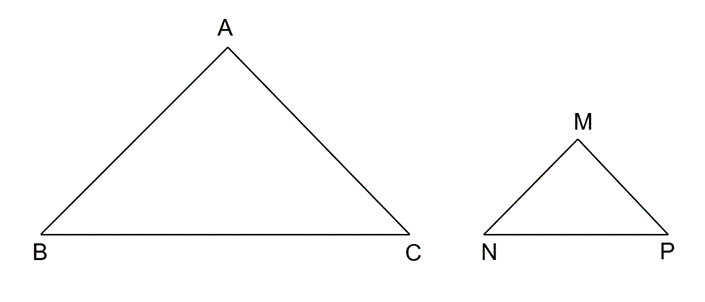
Cho tam giác ABC cân tại đỉnh A và tam giác MNP cân tại đỉnh M. Biết rằng \(\widehat {BAC} = \widehat {PMN}\), AB=2MN. Chứng minh ΔMNP ∽ ΔABC và tìm tỉ số đồng dạng
Phương pháp giải - Xem chi tiết
Sử dụng tam giác ABC cân tại A, tam giác MNP cân tại M để chứng minh ΔMNP ∽ ΔABC và tìm tỉ số đồng dạng của chúng.
Lời giải chi tiết
- Có tam giác ABC cân tại A => AB = AC, \(\widehat B = \widehat C\)
- Có tam giác MNP cân tại M => MN = MP, \(\widehat N = \widehat P\)
Mà AB = 2MN, \(\widehat A = \widehat M\)
=> \(\widehat B = \widehat N = \widehat C = \widehat P\)
\( \Rightarrow \frac{{MN}}{{AB}} = \frac{{MP}}{{AC}} = \frac{{NP}}{{BC}} = \frac{1}{2}\)
=> ΔMNP ∽ ΔABC với tỉ số đồng dạng là \(\frac{1}{2}\)
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 9.4 trang 82 SGK Toán 8 tập 2 - Kết nối tri thức timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 9.4 trang 82 SGK Toán 8 tập 2 - Kết nối tri thức timdapan.com"







