Giải bài 9.31 trang 83 SGK Toán 7 tập 2 - Kết nối tri thức
Chứng minh rằng tam giác có đường trung tuyến và đường cao xuất phát từ cùng một đỉnh trùng nhau là một tam giác cân.
Đề bài
Chứng minh rằng tam giác có đường trung tuyến và đường cao xuất phát từ cùng một đỉnh trùng nhau là một tam giác cân.
Phương pháp giải - Xem chi tiết
-Chứng minh \(\Delta ABD = \Delta ACD\left( {c - g - c} \right)\)
Lời giải chi tiết
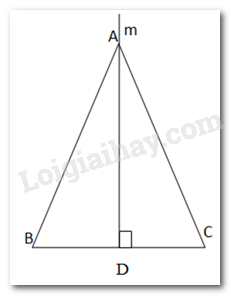
Từ A kẻ đường thẳng m vuông góc với BC tại trung điểm D của BC.
\( \Rightarrow \) AD là đường trung tuyến của BC.
Xét \(\Delta ABD\) và \(\Delta ACD\) có:
\(\begin{array}{l}\widehat {ADB} = \widehat {ADC} = {90^0}\\AD:chung\\BD = CD\left( {gt} \right)\\ \Rightarrow \Delta ABD = \Delta ACD\left( {c - g - c} \right)\end{array}\)
\( \Rightarrow AB = AC\)(2 cạnh tương ứng)
\( \Rightarrow \Delta ABC\)cân tại A (đpcm).
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 9.31 trang 83 SGK Toán 7 tập 2 - Kết nối tri thức timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 9.31 trang 83 SGK Toán 7 tập 2 - Kết nối tri thức timdapan.com"







