Bài 9.1, 9.2, 9.3 phần bài tập bổ sung trang 96, 97 SBT toán 6 tập 2

Bài 9.1

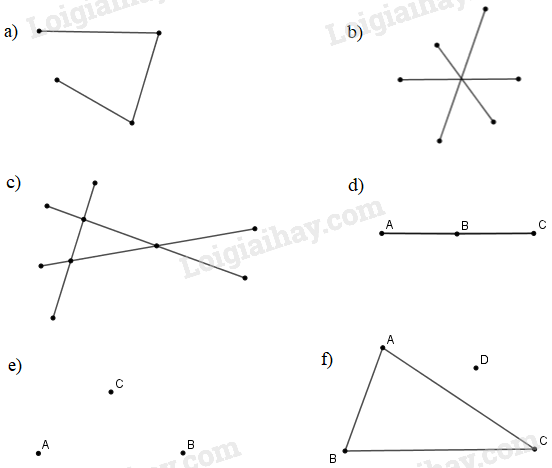
Vẽ hình để thấy được mỗi câu sau đây là sai :

a) Hình gồm \(3\) đoạn thẳng được gọi là tam giác

b) Hình gồm \(3\) đoạn thẳng đôi một cắt nhau được gọi là tam giác.

c) Hình gồm \(3\) đoạn thẳng đôi một cắt nhau tạo ra \(3\) giao điểm (phân biệt) được gọi là tam giác.

d) Hình gồm \(3\) đoạn thẳng \(AB, BC, CA\) được gọi là tam giác \(ABC\).

e) Hình gồm \(3\) điểm không thẳng hàng \(A, B, C\) được gọi là tam giác \(ABC\).

f) Một điểm không thuộc cạnh của tam giác \(ABC \) thì phải nằm trong tam giác đó;

g) Một điểm không phải là đỉnh của tam giác \(ABC\) thì phải nằm trong tam giác đó.

h) Một điểm không nằm bên trong tam giác \(ABC\) thì phải nằm ngoài tam giác đó.

i) Hình gồm \(2\) góc được gọi là tam giác.

j) Hình gồm \(3\) góc mà các cạnh của nó đôi một cắt nhau tạo ra ba điểm được gọi là tam giác.

Phương pháp giải:

Dùng thước thẳng và compa để vẽ hình

Giải chi tiết:

Bài 9.2

Vẽ hình liên tiếp theo cách diễn đạt sau đây

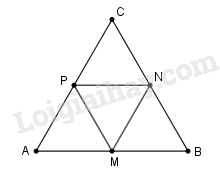
a) Vẽ tam giác \(ABC\), có \(AB = 6cm,\) \(BC = 6cm, CA = 6cm.\)

b) Vẽ tiếp các điểm \(M, N, P\) tương ứng là trung điểm của các đoạn thẳng \(AB, BC, CA.\)

c) Vẽ tiếp tam giác \(MNP.\)

d) Đọc tên các góc, các cạnh của những tam giác có \(3\) đỉnh lấy trong số các điểm \(A, B, C, M, N, P.\)

Phương pháp giải:

Dùng thước thẳng và compa để vẽ hình từ đó đọc tên các góc và các cạnh của tam giác

Giải chi tiết:

Ta có hình bs.20  

Bài 9.3

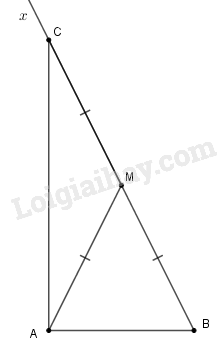
a) Vẽ tam giác \(ABM\) có \(AB = 5cm,\) \(BM = AM = 6,5cm;\)

b) Vẽ tiếp góc \(Amx\) kề bù với góc \(AMB;\)

c) Vẽ tam giác \(AMC\), sao cho \(MA = MC\) và điểm \(C\) thuộc tia \(Mx;\)

d) So sánh \(MB, MA, MC;\)

e) Cho biết độ dài của đoạn thẳng \(BC;\)

f) Đo và cho biết số đo của góc \(BAC;\)

g) Đo và cho biết độ dài của đoạn thẳng \(AC.\)

Phương pháp giải:

Dùng thước thẳng và compa để vẽ hình

Từ đó đo độ dài của cạnh và góc

Giải chi tiết:

Sau khi ta vẽ được hình bs.21

d) Ta có \(MA = MB = MC = 6,5cm.\)

e) Do \(C\) thuộc tia đối của tia \(MB\) nên điểm \(M\) ở giữa hai điểm \(B\) và \(C\) đồng thời \(MB = MC = 5,6cm\) nên \(M\) là trung điểm của \(BC\). Từ đó \(BC = 13cm.\)

f) Dùng thước đo góc, ta có \(\widehat {BAC} = 90^\circ .\)

g) Sau khi đo đoạn thẳng \(AC\) có độ dài là \(12cm.\)