Bài 9 trang 117 Vở bài tập toán 9 tập 1

Đề bài

Cho đường tròn tâm O bán kính 5cm, dây AB bằng 8cm.

a) Tính khoảng cách từ tâm O đến dây AB

b) Gọi I là điểm thuộc dây AB sao cho \(AI = 1cm.\) Kẻ dây CD đi qua I và vuông góc với AB. Chứng minh rằng \(CD  = AB.\)

Lời giải chi tiết

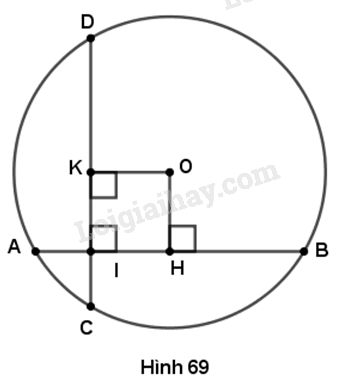
a) Kẻ \(OH \bot AB.\) Đường kính chứa \(OH\) vuông góc với \(AB\) nên \(AH = HB = AB:2 \)\(= 8:2 = 4\left( {cm} \right).\)

Tính \(OH:\) Áp dụng định lí Py-ta-go, ta có :

\(O{H^2} = O{A^2} - A{H^2} = {5^2} - {4^2} = 9\) nên \(OH = 3cm.\)

b) Kẻ \(OK \bot CD.\) Tứ giác \(OKIH\) có \(\widehat K = \widehat I \)\(= \widehat H = {90^o}\) nên là hình chữ nhật.

Do đó \(OK = IH = AH - AI \)\(= 4 - 1 = 3\left( {cm} \right).\)

Ta có \(OK = OH\) nên \(AB = CD\) (hai dây cách đều tâm thì bằng nhau).