Giải bài 7.50 trang 58 SGK Toán 8 tập 2 - Kết nối tri thức

Đề bài

Cho hàm số bậc nhất y=(m+2)x+3

a) Tìm m để đồ thị hàm số song song với đường thẳng y=−x

b) Vẽ đồ thị hàm số với giá trị m tìm được ở câu a

c) Tìm giao điểm A của đồ thị hàm số tìm được ở câu a và đồ thị của hàm số y=x+1. Tính diện tích của tam giác OAB, trong đó B là giao điểm của đồ thị hàm số y=x+1 với trục Ox

Lời giải chi tiết

a)Hai đường thẳng song song với nhau khi:

m+2=−1

m=−3

b) Đồ thị hàm số y=−x+3 là đường thẳng đi qua 2 điểm (0;3) và (3;0)

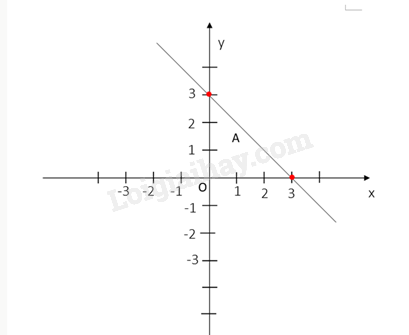
c) Đồ thị hàm số y=x+1 là đường thẳng đi qua 2 điểm (0;1) và (-1;0)

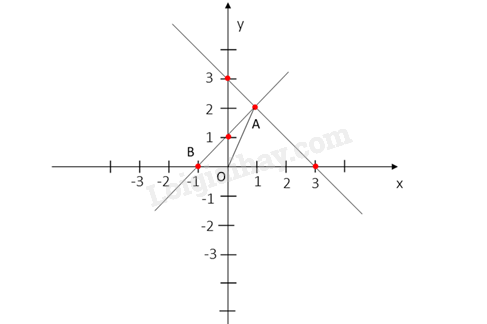
 Có A(1; 2); B(-1; 0); C(0; 0)

\(\begin{array}{l} \Rightarrow AB = \sqrt {{{( - 1 - 1)}^2} + {{\left( {0 - 2} \right)}^2}}  = 2\sqrt 2 \\OA = \sqrt {{{\left( {1 - 0} \right)}^2} + {{\left( {2 - 0} \right)}^2}}  = \sqrt 5 \\OB = \sqrt {{{\left( { - 1 - 0} \right)}^2}}  = 1\end{array}\)

Gọi C là giao điểm của đồ thị hàm số y  = - x + 3 với trục Ox

Có C(3; 0)

\(\begin{array}{l} \Rightarrow AC = \sqrt {{{\left( {3 - 1} \right)}^2} + {{\left( {0 - 2} \right)}^2}}  = 2\sqrt 2 \\ \Rightarrow BC = \sqrt {{{\left( {3 + 1} \right)}^2}}  = 4\\ \Rightarrow OC = 3\end{array}\)

Suy ra tam giác ABC vuông tại A

Diện tích tam giác ABC là: \(\frac{1}{2}{\left( {2\sqrt 2 } \right)^2} = 4\)

Diện tích tam giác OAC là: \(\frac{1}{2}.2.3 = 3\)

Diện tích tam giác OAB là: \({S_{ABC}} - S{}_{OAC} = 4 - 3 = 1\)