Bài 64 trang 87 SBT toán 8 tập 1
Giải bài 64 trang 87 sách bài tập toán 8. Chứng minh rằng điểm I đối xứng với điểm K qua AH...
Đề bài
Cho tam giác \(ABC\) cân tại \(A,\) đường cao \(AH.\) Trên cạnh \(AB\) lấy điểm \(I,\) trên cạnh \(AC\) lấy điểm \(K\) sao cho \(AI = AK.\) Chứng minh rằng điểm \(I\) đối xứng với điểm \(K\) qua \(AH.\)
Phương pháp giải - Xem chi tiết
+) Sử dụng định nghĩa: Hai điểm gọi là đối xứng với nhau qua đường thẳng \(d\) nếu \(d\) là đường trung trực của đoạn thẳng nối hai điểm đó.
+) Trong tam giác cân, đường trung tuyến ứng với cạnh đáy cũng là đường trung trực, đường phân giác.
Lời giải chi tiết
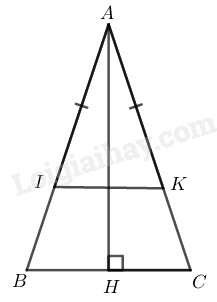
\(∆ ABC\) cân tại \(A\)
\(AH ⊥ BC\;\; (gt)\)
Suy ra : \(AH\) là tia phân giác \(\widehat A\)
\(AI = AK\;\; (gt)\)
\(⇒∆ AIK\) cân tại \(A\)
\(AH\) là tia phân giác \(\widehat A\)
nên \(AH\) là đường trung trực của \(IK\)
Vậy \(I\) đối xứng với \(K\) qua \(AH.\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 64 trang 87 SBT toán 8 tập 1 timdapan.com"







