Bài 5.10 trang 16 SBT Vật lí 7
Giải bài 5.10 trang 16 sách bài tập vật lí 7. Một điểm sáng s đặt trước một gương phẳng OM (hình 5.5).
Đề bài
Một điểm sáng \(S\) đặt trước một gương phẳng \(OM\) (hình 5.5). Khi gương quay thì cho ảnh của \(S\) di chuyển trên đường nào? Gương quay một góc \(30^0\) quanh \(O\) thì ảnh của \(S\) di chuyển như thế nào? Đoạn thẳng \(OS’\) quay được một góc bằng bao nhiêu?
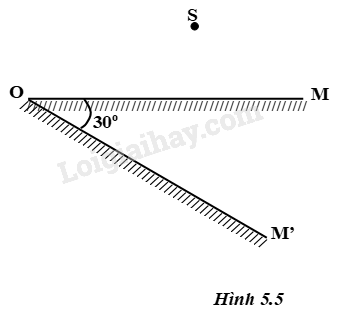
Phương pháp giải - Xem chi tiết
Sử dụng lí thuyết tính chất ảnh tạo bởi gương phẳng
Sử dụng lí thuyết định luật phản xạ ánh sáng
Lời giải chi tiết
+ Khi gương quay ở vị trí \(OM\) thì cho ảnh của \(S\) là \(S'\), ta có \(SI = {\rm{IS'}}\) và hai góc bằng nhau: \(\widehat {SOI} = \widehat {IOS'}\)
+ Khi gương quay đến quanh điểm \(O\) đến vị trí \(OM'\) cho ảnh \(S''\), ta có \(SK = KS''\) và \(\widehat {SOK} = \widehat {KOS''}\)
Như vậy, khi gương quay một góc \(\widehat {MOM'} = \alpha \) thì ảnh quay một góc \(\beta = \widehat {S'OS''}\)
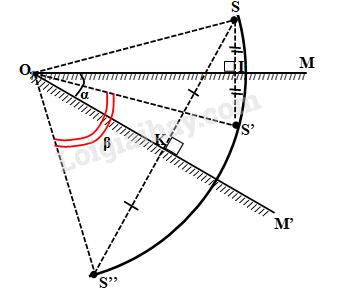
Theo hình vẽ, ta có:
\(\beta = \widehat {S'OS''} = \widehat {S'OK} + \widehat {KOS''}\)
Mà
\(\begin{array}{l}\widehat {S'OK} = \widehat {MOM'} - \widehat {IOS'}\\ = \alpha - \widehat {IOS'} = \alpha - \widehat {IOS}\end{array}\)
Do đó:
\(\begin{array}{l}\beta = \alpha - \widehat {IOS} + \widehat {KOS''} = \alpha + (\widehat {KOS} - \widehat {IOS})\\ = \alpha + \widehat {MOM'} = \alpha + \alpha = 2\alpha \end{array}\)
Vậy khi gương quay góc \(\alpha \) thì đường nối ảnh với \(O\) quay được góc \(\beta = 2\alpha \)
Vì \({\rm{OS = OS' = OS}}''\) nên ảnh di chuyển trên một cung tròn có bán kính \({\rm{OS = OS' = OS}}''\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 5.10 trang 16 SBT Vật lí 7 timdapan.com"







