Giải bài 49 trang 54 sách bài tập toán 7 - Cánh diều
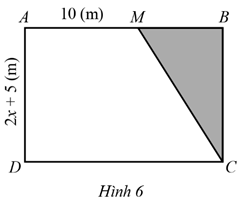
Một mảnh đất có dạng hình thang vuông với đáy bé là 10 m, chiều cao là 2x + 5 (m). Người ta mở rộng mảnh đất đó để được mảnh đất có dạng hình chữ nhật như Hình 6. Biết diện tích của phần đất mở rộng (phần tô đậm) là 6x2 + 13x – 5 (m2), tính diện tích của mảnh đất lúc ban đầu.
Đề bài
Một mảnh đất có dạng hình thang vuông với đáy bé là 10 m, chiều cao là 2x + 5 (m). Người ta mở rộng mảnh đất đó để được mảnh đất có dạng hình chữ nhật như Hình 6. Biết diện tích của phần đất mở rộng (phần tô đậm) là 6x2 + 13x – 5 (m2), tính diện tích của mảnh đất lúc ban đầu.
Phương pháp giải - Xem chi tiết
Bước 1: Lập công thức tính diện tích phần đất mở rộng \(\left( {S = \frac{1}{2}BM.BC} \right)\) và tính độ dài BM theo x
Bước 2: Tính diện tích hình thang vuông biết độ dài đáy nhỏ AM, đáy lớn CD = AB, chiều cao AD
Lời giải chi tiết
Ta có: \({S_{BCM}} = \frac{1}{2}BM.BC = \frac{1}{2}.BM.(2x + 5) = 6{x^2} + 13x - 5\) (m2)
Suy ra \(BM = 2(6{x^2} + 13x - 5):(2x + 5) = (12{x^2} + 26x - 10):(2x + 5)\)
Đặt tính chia ta được \(BM = 6x - 2\) (m)
Khi đó \(AB = CD = AM + BM = 10 + (6x - 2) = 6x + 8\) (m)
Vậy diện tích mảnh đất hình thang vuông là:
\({S_{AMCD}} = \frac{1}{2}.AD.(AM + CD) = \frac{1}{2}.(2x + 5).(10 + 6x + 8) = \frac{1}{2}(2x + 5)(6x + 18)\)
\( = \frac{1}{2}(12{x^2} + 36x + 30x + 90) = \frac{1}{2}(12{x^2} + 66x + 90) = 6{x^2} + 33x + 45\) (m2)
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 49 trang 54 sách bài tập toán 7 - Cánh diều timdapan.com"







