Bài 46 trang 81 Vở bài tập toán 7 tập 1
Giải bài 46 trang 81 VBT toán 7 tập 1. Vẽ trên cùng một hệ trục tọa độ đồ thị của các hàm số: a) y = - x ...
Đề bài
Vẽ trên cùng một hệ trục tọa độ đồ thị của các hàm số:
a) \(y = -x\);
b) \(y = \dfrac{1}{2}x\);
c) \(y = - \dfrac{1}{2}x\).
Phương pháp giải - Xem chi tiết
Đồ thị của hàm số \(y=ax\;(a\ne 0)\) là đường thẳng đi qua gốc tọa độ \(O\). Với mỗi hàm số trên ta chỉ cần lấy thêm điểm \(A\) (khác \(O\)) thuộc hàm số đó, đồ thị của hàm số đã cho là đường thẳng \(OA\).
Lời giải chi tiết
Các hàm số trên đều có dạng \(y=ax\;(a\ne 0)\) nên đồ thị của chúng là đường thẳng đi qua gốc tọa độ. Để vẽ đồ thị của mỗi hàm số trên như sau:
Cho \(x\) một giá trị và thay vào công thức biểu diễn hàm số tương ứng để xác định giá trị của \(y\). Đồ thị của hàm số cần vẽ là đường thẳng đi qua điểm vừa xác định và gốc tọa độ.
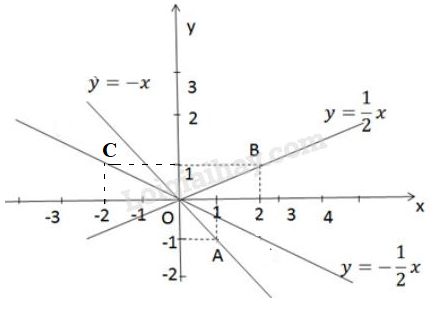
a) Vẽ đồ thị của hàm số \(y=-x\). Xác định điểm \(A\): Cho \(x = 1\) thay vào công thức trên ta có \(y = -1\). Vậy đồ thị của \(y=-x\) là đường thẳng đi qua \(A (1;-1)\) và \(O(0;0)\) được vẽ trong hình 17.
b) Vẽ đồ thị của hàm số \(y = \dfrac{1}{2}x\). Xác địn điểm \(B\): Cho \(x=2\) thay vào công thức trên ta có \(y= \dfrac{1}{2}.2=1\). Vậy đồ thị của hàm số \(y = \dfrac{1}{2}x\) là đường thẳng đi qua \(B(2;1)\) và \(O(0;0)\) được vẽ trong hình \(17.\)
c) Vẽ đồ thị của hàm số \(y = - \dfrac{1}{2}x\)
Xác định điểm \(C\): Cho \(x=-2\) thay vào công thức trên ta có \(y=- \dfrac{1}{2}.(-2)=1\). Vậy đồ thị của hàm số \(y = -\dfrac{1}{2}x\) là đường thẳng đi qua \(C(-2;1)\) và \(O(0;0)\) được vẽ trong hình \(17.\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 46 trang 81 Vở bài tập toán 7 tập 1 timdapan.com"







