Bài 38 trang 113 Vở bài tập toán 9 tập 2

Đề bài

a) Vẽ đường tròn tâm O, bán kính 2 cm.

b) Vẽ hình vuông nội tiếp đường tròn (O) ở câu a).

c) Tính bán kính r của đường tròn nội tiếp hình vuông ở câu b) rồi vẽ đường tròn (O ; r).

Lời giải chi tiết

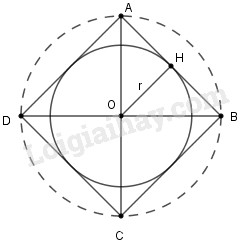
a)  Lấy điểm \(O\) làm tâm, vẽ đường tròn có tâm \(O\) và bán kính \(R = 2cm.\)

b) Kẻ hai đường kính \(AC\) và \(BD\) vuông góc với nhau. Nối \(AB,BC,CD,DA\) ta được hình vuông \(ABCD\) nội tiếp đường tròn \(\left( O \right).\)

c) Kẻ \(OH \bot AB\). \(OH\) là bán kính \(r\) của đường tròn nội tiếp hình vuông \(ABCD.\)

Xét \(\Delta AOB\) là tam giác vuông cân tại \(O\) và \(OH \bot AB\) nên \(OH\) là vừa là đường cao vừa là đường trung tuyến của \(\Delta AOB.\)

Suy ra \(OH = HA = HB\,\left( 1 \right)\). Do đó,  \(O{A^2} = O{H^2} + A{H^2},\) hay \(O{A^2} = 2.{r^2}.\)

Mà \(OA = 2 \Rightarrow r = \sqrt 2 .\)

Vẽ đường tròn \(\left( {O;r} \right)\) là đường tròn nội tiếp hình vuông \(ABCD\) vì tiếp xúc với bốn cạnh của hình vuông.